In natural-language understanding (NLU), the Transformer-based BERT language model is king. Its high performance on multiple tasks has strongly influenced contemporary NLU research.
On the other hand, it is a relatively big and slow model, which makes it unsuitable for some applications. Multiple efforts have been made to compress the BERT architecture, but the choice of architectural parameters (the number of layers, the number of processing nodes per layer, and so on) has been somewhat arbitrary, and the resulting models are rarely much better than the original at optimizing the balance between the model’s size, speed, and error rate.
A few weeks ago, we released part of the code for Bort, a highly optimized language model (LM) extracted from the BERT architecture through a combination of two rigorous algorithmic techniques especially designed for neural-network compression.
We tested Bort on 23 NLU tasks, and on 20 of them, it improved on BERT’s performance — by 31% in one case — even though it’s 16% the size and about 20 times as fast.
The code doesn’t contain the full versions of the algorithms we used to extract Bort from BERT, but I will discuss them here briefly.
Principled approach
A solid understanding of the intrinsic difficulty of a problem allows us to design efficient and correct algorithms for solving that problem that can be trusted to perform consistently. Think of trying to sort an array of numbers by just trying out random permutations: this approach will quickly become intractable as the size of the input grows. Thankfully, sorting is a well-studied problem with fast and correct solutions and a nicely bounded runtime growth. Why can’t compressing BERT, or any network, be the same way?
We wanted to produce a version of BERT whose architectural parameters minimized its parameter size, inference speed, and error rate, and I wanted to show that these architectural parameters were optimal. I call this problem “optimal subarchitecture extraction”, or OSE. Note that this is a different compression approach than weight pruning, which heuristically removes connections from a previously trained network.
An algorithm solving OSE should also work for any input, not just BERT; a general-purpose algorithm would save a lot of time — and GPU cycles — otherwise spent on trial and error approaches.
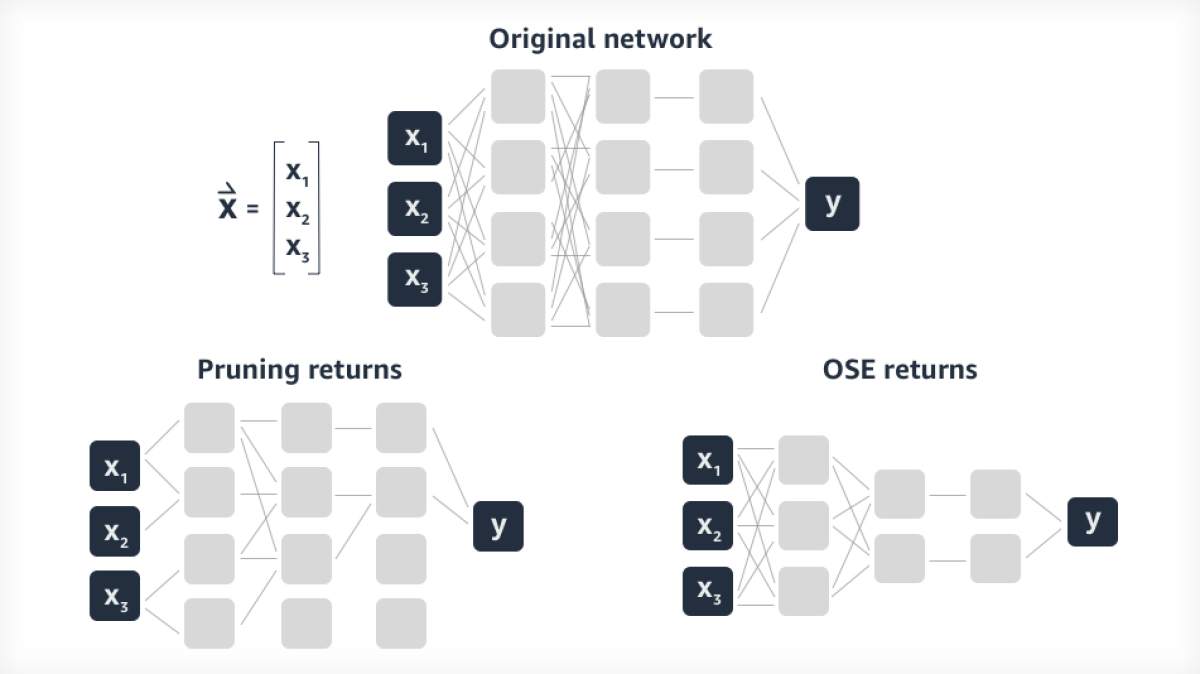
OSE is a computationally hard problem, so the best we can hope for is an algorithm that returns something in the ballpark of the optimum. But even a ballpark algorithm could be impractically time consuming with a large enough input.
My research showed that there is an efficient algorithm for extracting a subarchitecture whose functions — parameter size, inference speed, and error rate — have a polynomial correlation with the architectural parameters, meaning that they’re bounded by some polynomial function of the architectural parameters.
This is easy to see for the parameter size of the network, since it boils down to a counting argument based on the number of nodes per layer, times the number of layers (see image caption above). The same argument can be made for the inference speed — the rate at which a network outputs a result given an input — as it is related to the parameter size.
Under some circumstances, the algorithm’s error rate has a similar correlation. Furthermore, whenever the “cost” associated with the first (call it A) and last layers of the network is lower than that of the middle layers (B), the runtime of a solution will not explode. I call all these assumptions the ABnC property, which BERT turns out to have.
For inputs having the ABnC property, the algorithm I designed behaves like a fully polynomial-time approximation scheme, or FPTAS. Being an FPTAS means that an approximation parameter — which defines how far short of the optimal solution you’re willing to fall — can now be given as an input to the algorithm, and the algorithm’s execution time depends polynomially on that parameter.
The more accurate you want the approximation to be, the longer the algorithm takes to execute. But at least the trade-off can be precisely specified, and the runtime of the algorithm is guaranteed to not grow too quickly.
I ran the FPTAS on BERT and obtained a set of architectural parameters (Bort), and from the proofs we knew that it would be Pareto optimal. That is, it optimized the balance between inference speed, parameter size, and error rate: a faster model would necessarily be bigger or more error prone; a more accurate model would be larger or slower. Any model that broke that balance would necessarily be suboptimal.
Generalizability
The true strength of BERT lies in its generalizability across tasks. BERT learns to represent words of a language as points in a shared space, where proximity in the space implies semantic similarity. That general model can then be fine-tuned on specific tasks, such as question answering or text classification.
To see whether Bort generalizes as well as BERT, we needed to pre-train it and then test it on several different natural-language-understanding tasks. The FPTAS doesn’t return a trained model, and it didn’t know that our ultimate goal was fine-tuning.
When fine-tuning, I opted to follow BERT’s approach and attach a single linear classifier to Bort. I supposed that a good LM would have no problems with this setup, but the fine-tuning process was hard, and several variations on this strategy (e.g., knowledge distillation, deeper classifiers, and hyperparameter search) failed to yield a model that reached the theoretical limits predicted by the FPTAS.
In machine learning, it is crucial to have a good selection of features to make the data representative of the task, which in turn makes the task learnable. Deep networks operate in a hierarchical fashion, which makes them fantastic at selecting features automatically. If the model is too small and the data too scarce, however, the task may not be learnable. And Bort is, by design, a small model.
The Agora algorithm
To address this problem, I developed a second algorithm, called Agora, which leverages the development set for the task Bort is being fine-tuned on. In machine learning, a labeled data set is usually split into three components: the training set is used to train a model; the development (or dev) set is used to check for over-/underfitting; and the test set is used to assess the model’s generalizability.
With Agora, Bort is first fine-tuned on the training set, then applied to the data in the dev set. Agora finds the data points in the dev set that the pretrained Bort model labeled incorrectly and samples new points near them in a chosen representation space. Those samples are labeled by a second model, and then they’re added into the training set.
It might sound silly to add randomized points from the dev set to the training set. You might expect the fine-tuned model to overfit the dev set data, so that it doesn’t generalize well to unfamiliar inputs — which means that it didn’t actually learn.
But this is a powerful approach to situations with scarce or ill-formed data. The proof of this is non-trivial, but intuitively, this algorithm works because it “reconstructs” the input in a way that is equivalent, in a precise sense, to the distribution of the task we are modeling in the first place. I believe the best part about Agora is not its effectiveness but that it is another proof of what the great Patrick Winston showed fifty years ago: you can’t learn something that you do not already know almost completely.

The application of both algorithms to BERT yielded Bort, which has an effective (not counting the embedding layer) size of 5.5% of the original BERT architecture and a net size of 16%. The effective size is more important because the first layer, by the ABnC property, is not as expensive as the other layers when performing inference. Indeed, Bort is up to 20 times faster, on a CPU, than BERT. It is also able to be pretrained much more rapidly than usual — likely due to the FPTAS’s preferring faster-converging architectures. It also obtained improvements of up to 31%, absolute, with respect to BERT, across multiple NLU benchmarks.
Acknowledgments: Daniel J. Perry, my coauthor for the Bort paper.

















