Today we are happy to announce Ocelot, our first-generation quantum chip. Ocelot represents Amazon Web Services’ pioneering effort to develop, from the ground up, a hardware implementation of quantum error correction that is both resource efficient and scalable. Based on superconducting quantum circuits, Ocelot achieves the following major technical advances:
- The first realization of a scalable architecture for bosonic error correction, surpassing traditional qubit approaches to reducing error correction overhead;
- The first implementation of a noise-biased gate — a key to unlocking the type of hardware-efficient error correction necessary for building scalable, commercially viable quantum computers;
- State-of-the-art performance for superconducting qubits, with bit-flip times approaching one second in tandem with phase-flip times of 20 microseconds.

We believe that scaling Ocelot to a full-fledged quantum computer capable of transformative societal impact would require as little as one-tenth as many resources as common approaches, helping bring closer the age of practical quantum computing.
The quantum performance gap
Quantum computers promise to perform some computations much faster — even exponentially faster — than classical computers. This means quantum computers can solve some problems that are forever beyond the reach of classical computing.
Practical applications of quantum computing will require sophisticated quantum algorithms with billions of quantum gates — the basic operations of a quantum computer. But current quantum computers’ extreme sensitivity to environmental noise means that the best quantum hardware today can run only about a thousand gates without error. How do we bridge this gap?
Quantum error correction: the key to reliable quantum computing
Quantum error correction, first proposed theoretically in the 1990s, offers a solution. By sharing the information in each logical qubit across multiple physical qubits, one can protect the information within a quantum computer from external noise. Not only this, but errors can be detected and corrected in a manner analogous to the classical error correction methods used in digital storage and communication.
Recent experiments have demonstrated promising progress, but today’s best logical qubits, based on superconducting or atomic qubits, still exhibit error rates a billion times larger than the error rates needed for known quantum algorithms of practical utility and quantum advantage.
The challenge of qubit overhead
While quantum error correction provides a path to bridging the enormous chasm between today’s error rates and those required for practical quantum computation, it comes with a severe penalty in terms of resource overhead. Reducing logical-qubit error rates requires scaling up the redundancy in the number of physical qubits per logical qubit.
Traditional quantum error correction methods, such as those using the surface error-correcting code, currently require thousands (and if we work really, really hard, maybe in the future, hundreds) of physical qubits per logical qubit to reach the desired error rates. That means that a commercially relevant quantum computer would require millions of physical qubits — many orders of magnitude beyond the qubit count of current hardware.
One fundamental reason for this high overhead is that quantum systems experience two types of errors: bit-flip errors (also present in classical bits) and phase-flip errors (unique to qubits). Whereas classical bits require only correction of bit flips, qubits require an additional layer of redundancy to handle both types of errors.
Although subtle, this added complexity leads to quantum systems’ large resource overhead requirement. For comparison, a good classical error-correcting code could realize the error rate we desire for quantum computing with less than 30% overhead, roughly one-ten-thousandth the overhead of the conventional surface code approach (assuming bit error rates of 0.5%, similar to qubit error rates in current hardware).
Cat qubits: an approach to more efficient error correction
Quantum systems in nature can be more complex than qubits, which consist of just two quantum states (usually labeled 0 and 1 in analogy to classical digital bits). Take for example the simple harmonic oscillator, which oscillates with a well-defined frequency. Harmonic oscillators come in all sorts of shapes and sizes, from the mechanical metronome used to keep time while playing music to the microwave electromagnetic oscillators used in radar and communication systems.
Classically, the state of an oscillator can be represented by the amplitude and phase of its oscillations. Quantum mechanically, the situation is similar, although the amplitude and phase are never simultaneously perfectly defined, and there is an underlying graininess to the amplitude associated with each quanta of energy one adds to the system.
These quanta of energy are what are called bosonic particles, the best known of which is the photon, associated with the electromagnetic field. The more energy we pump into the system, the more bosons (photons) we create, and the more oscillator states (amplitudes) we can access. Bosonic quantum error correction, which relies on bosons instead of simple two-state qubit systems, uses these extra oscillator states to more effectively protect quantum information from environmental noise and to do more efficient error correction.
One type of bosonic quantum error correction uses cat qubits, named after the dead/alive Schrödinger cat of Erwin Schrödinger's famous thought experiment. Cat qubits use the quantum superposition of classical-like states of well-defined amplitude and phase to encode a qubit’s worth of information. Just a few years after Peter Shor’s seminal 1995 paper on quantum error correction, researchers began quietly developing an alternative approach to error correction based on cat qubits.
A major advantage of cat qubits is their inherent protection against bit-flip errors. Increasing the number of photons in the oscillator can make the rate of the bit-flip errors exponentially small. This means that instead of increasing qubit count, we can simply increase the energy of an oscillator, making error correction far more efficient.
The past decade has seen pioneering experiments demonstrating the potential of cat qubits. However, these experiments have mostly focused on single-cat-qubit demonstrations, leaving open the question of whether cat qubits could be integrated into a scalable architecture.
Ocelot: demonstrating the scalability of bosonic quantum error correction
Today in Nature, we published the results of our measurements on Ocelot, and its quantum error correction performance. Ocelot represents an important step on the road to practical quantum computers, leveraging chip-scale integration of cat qubits to form a scalable, hardware-efficient architecture for quantum error correction. In this approach,
- bit-flip errors are exponentially suppressed at the physical-qubit level;
- phase-flip errors are corrected using a repetition code, the simplest classical error-correcting code; and
- highly noise-biased controlled-NOT (C-NOT) gates, between each cat qubit and ancillary transmon qubits (the conventional qubit used in superconducting quantum circuits), enable phase-flip-error detection while preserving the cat’s bit-flip protection.
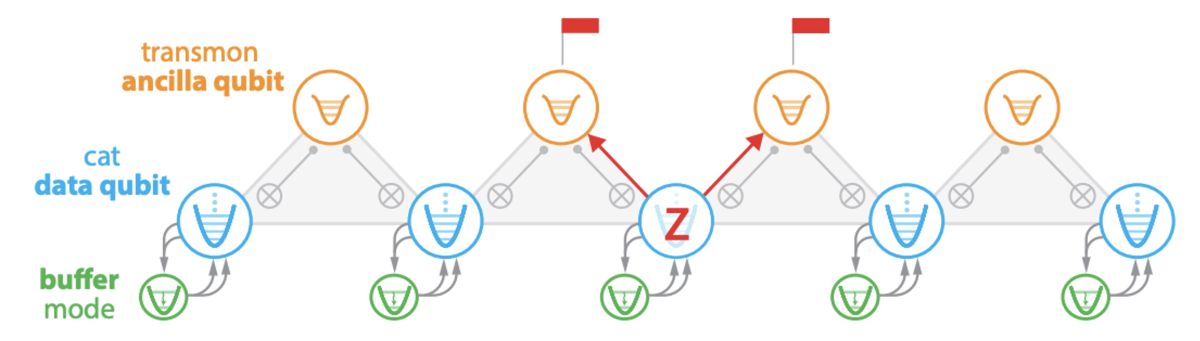
The Ocelot logical-qubit memory chip, shown schematically above, consists of five cat data qubits, each housing an oscillator that is used to store the quantum data. The storage oscillator of each cat qubit is connected to two ancillary transmon qubits for phase-flip-error detection and paired with a special nonlinear buffer circuit used to stabilize the cat qubit states and exponentially suppress bit-flip errors.
Tuning up the Ocelot device involves calibrating the bit- and phase-flip error rates of the cat qubits against the cat amplitude (average photon number) and optimizing the noise-bias of the C-NOT gate used for phase-flip-error detection. Our experimental results show that we can achieve bit-flip times approaching one second, more than a thousand times longer than the lifetime of conventional superconducting qubits.
Critically, this can be accomplished with a cat amplitude as small as four photons, enabling us to retain phase-flip times of tens of microseconds, sufficient for quantum error correction. From there, we run a sequence of error correction cycles to test the performance of the circuit as a logical-qubit memory. In order to characterize the performance of the repetition code and the scalability of the architecture, we studied subsets of the Ocelot cat qubits, representing different repetition code lengths.
The logical phase-flip error rate was seen to drop significantly when the code distance was increased from distance-3 to distance-5 (i.e., from a code with three cat qubits to one with five) across a wide range of cat photon numbers, indicating the effectiveness of the repetition code.
When bit-flip errors were included, the total logical error rate was measured to be 1.72% per cycle for the distance-3 code and 1.65% per cycle for the distance-5 code. The comparability of the total error rate of the distance-5 code to that of the shorter distance-3 code, with fewer cat qubits and opportunities for bit-flip errors, can be attributed to the large noise bias of the C-NOT gate and its effectiveness in suppressing bit-flip errors. This noise bias is what allows Ocelot to achieve a distance-5 code with less than a fifth as many qubits — five data qubits and four ancilla qubits, versus 49 qubits for a surface code device.
What we scale matters
From the billions of transistors in a modern GPU to the massive-scale GPU clusters powering AI models, the ability to scale efficiently is a key driver of technological progress. Similarly, scaling the number of qubits to accommodate the overhead required of quantum error correction will be key to realizing commercially valuable quantum computers.
But the history of computing shows that scaling the right component can have massive consequences for cost, performance, and even feasibility. The computer revolution truly took off when the transistor replaced the vacuum tube as the fundamental building block to scale.
Ocelot represents our first chip with the cat qubit architecture, and an initial test of its suitability as a fundamental building block for implementing quantum error correction. Future versions of Ocelot are being developed that will exponentially drive down logical error rates, enabled by both an improvement in component performance and an increase in code distance.
Codes tailored to biased noise, such as the repetition code used in Ocelot, can significantly reduce the number of physical qubits required. In our forthcoming paper “Hybrid cat-transmon architecture for scalable, hardware-efficient quantum error correction”, we find that scaling Ocelot could reduce quantum error correction overhead by up to 90% compared to conventional surface code approaches with similar physical-qubit error rates.
We believe that Ocelot's architecture, with its hardware-efficient approach to error correction, positions us well to tackle the next phase of quantum computing: learning how to scale. Using a hardware-efficient approach will allow us to more quickly and cost effectively achieve an error-corrected quantum computer that benefits society.
Over the last few years, quantum computing has entered an exciting new era in which quantum error correction has moved from the blackboard to the test bench. With Ocelot, we are just beginning down a path to fault-tolerant quantum computation. For those interested in joining us on this journey, we are hiring for positions across our quantum computing stack. Visit Amazon Jobs and enter the keyword “quantum”.

















