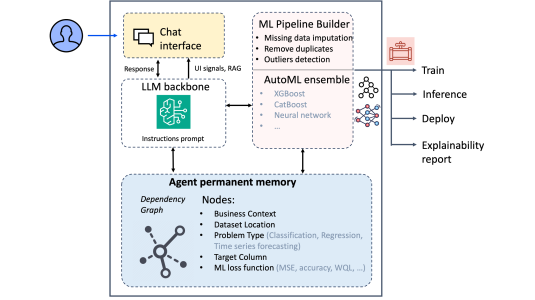
At the first annual Conference on Automated Machine Learning (AutoML), my colleagues and I won a best-paper award for a new way to decide when to terminate Bayesian optimization, a widely used hyperparameter optimization method.
Hyperparameters configure machine learning models, crucially affecting their performance. The depth and number of decision trees in a decision tree model or the number and width of the layers in a neural network are examples of hyperparameters. Optimizing hyperparameters requires retraining the model multiple times with different hyperparameter configurations to identify the best one.
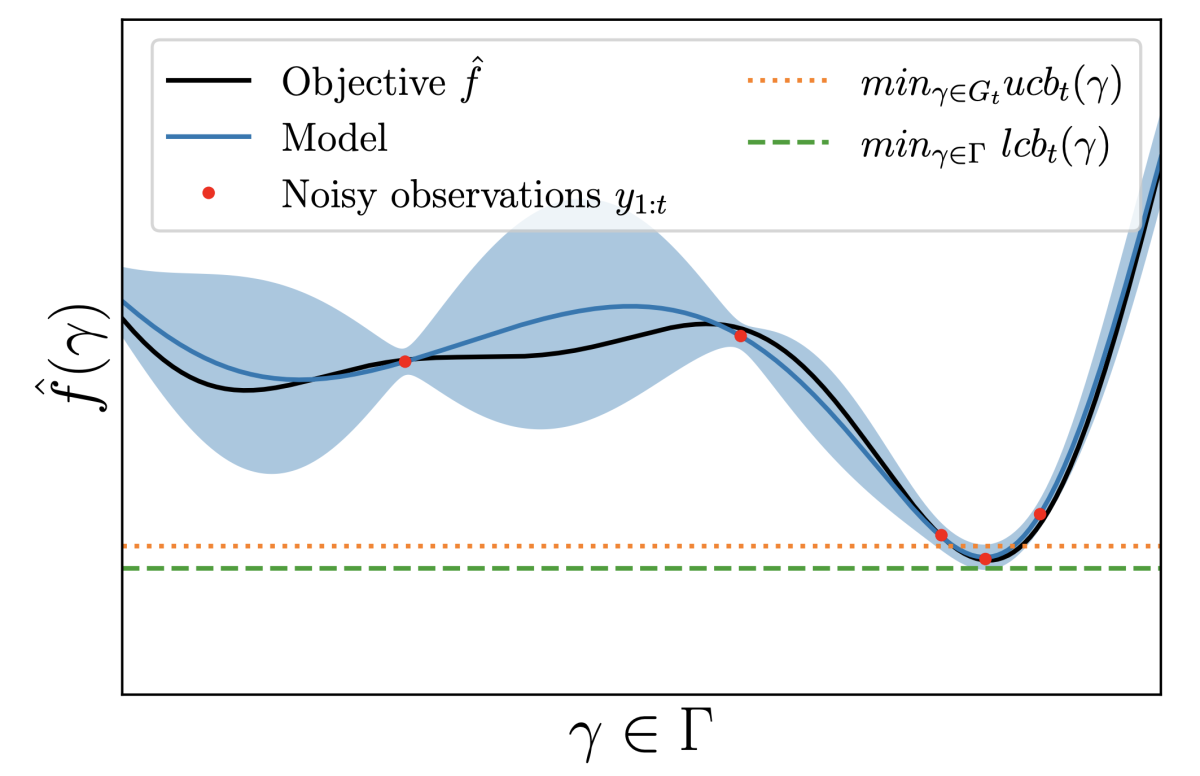
Usually, canvassing all possible hyperparameter configurations is prohibitively time consuming, so hyperparameter optimization (HPO) algorithms are designed to search the configuration space as efficiently as possible. Still, at some point the search has to be called off, and researchers have proposed a range of stopping criteria. For instance, a naive approach consists in terminating HPO if the best found configuration remains unchanged for some subsequent evaluations.
Our paper, “Automatic termination for hyperparameter optimization”, suggests a new principled stopping criterion, which, in our experiments, offered a better trade-off between the time consumption of HPO and the accuracy of the resulting models. Our criterion acknowledges the fact that the generalization error, which is the true but unknown optimization objective, does not coincide with the empirical estimate optimized by HPO. As a consequence, optimizing the empirical estimate too strenuously may in fact be counterproductive.
Convergence criterion for hyperparameter optimization
The goal of a machine learning model is to produce good predictions for unseen data. This means that a good model will minimize some generalization error, f. Population risk, for instance, measures the expected distance between the model’s prediction for a given input and the ground truth.
An HPO algorithm is always operating on some kind of budget — a restriction on the number of configurations it can consider, the wall clock time, the margin of improvement over the best configuration found so far, or the like. The algorithm’s goal is to minimize the distance between the ideal configuration, γ*, and the best configuration it can find before the budget is spent, γt*. That distance is known as the regret, rt:
rt= f(γt*) – f(γ*)
The regret quantifies the convergence of the HPO algorithm.
The quality of found configurations, however, is judged according to an empirical estimate of f, which we will denote by f-hat, or f with a circumflex accent over it (see figure, above). The empirical estimate is computed on the validation set, a subset of the model’s training data. If the validation set has a different distribution than the dataset as a whole, the empirical estimate is subject to statistical error, relative to relative to the true generalization error.
Our new stopping criterion is based on the observation that the accuracy of the evaluation of a particular hyperparameter configuration depends on the statistical error of the empirical estimate, f-hat. If the statistical error is greater than the regret, there’s no point in trying to optimize the configuration further. You could still improve performance on the validation set, but given the distributional mismatch, you might actually be hurting performance on the dataset as a whole.
The obvious difficulty with this approach is that we know neither the true regret — because we don’t know the model’s performance on the ideal hyperparameter configuration — nor the statistical error, because we don’t know how the validation set’s distribution differs from the full dataset’s.
Bounding the regret and estimation of the statistical error
The heart of our paper deals with establishing a stopping criterion when we know neither the regret nor the statistical error. Our work applies to Bayesian optimization (BO), which is an HPO method that is sample-efficient, meaning that it requires a relatively small number of hyperparameter evaluations.
First, we prove upper and lower bounds on the regret, based on the assumption that output values of the function relating hyperparameter configuration to performance follow a normal (Gaussian) distribution. This is, in fact, a standard assumption in HPO.
Then we estimate the statistical error of the empirical estimate, based on the statistical variance we observe during cross-validation. Cross-validation is a process in which the dataset is partitioned into a fixed number of equal subsets, and each subset serves in turn as the validation set, with the remaining subsets serving as training data. Cross-validation, too, is a common procedure in HPO.
Our stopping criterion, then, is that the statistical error exceeds the distance between the upper and lower bounds on the regret.
We test our approach against five baselines on two different decision tree models — XGBoost and random forest — and on a deep neural network, using two different datasets. Results vary, but on average, our approach best optimizes the trade-off between model accuracy and time spent on HPO.
The paper provides the technical details and the experiments we conducted to validate the termination criterion.