Knowledge graphs are data structures consisting of entities (the nodes of the graph) and relationships between them (the edges, usually depicted as line segments connecting nodes). The entities “Nile River” and “Africa”, for instance, might be connected in a knowledge graph by the relationship “is in”.
At Amazon, we use knowledge graphs to represent relationships between products and to encode information for Alexa’s question-answering service, among other things. Recently, we also built a knowledge graph that represented medical and biological information to help find treatments for COVID-19.
Today, many applications of knowledge graphs involve knowledge graph embedding, or representing the entities and relations in a knowledge graph as points in a vector space. To make knowledge graph embeddings easier to use, our team has released a set of tools called DGL-KE, for deep-graph-learning knowledge embeddings.
Last week at SIGIR, the Association for Computing Machinery’s annual conference on information retrieval, we presented a paper describing a set of optimizations that enable DGL-KE to run more efficiently in parallel-computing environments.
In experiments, our optimizations enabled DGL-KE to compute knowledge graph embeddings two to five times more efficiently than previous parallel-computing approaches did.
Geometric interpretation
The data encoded in a knowledge graph can be represented as sets of triplets; each triplet consists of a head entity, a relation, and a tail entity. For instance, in the triplet [Nile River | is in | Africa], “Nile River” is the head, “is in” the relation, and “Africa” the tail.
The standard way to embed a knowledge graph is with a machine learning model that takes entities and relations as inputs, and outputs fixed-length vectors. During training, the model is evaluated according to some score that relates the embeddings of the heads, relations, and tails of triplets.
For instance, the score might indicate how well the sum of the head and relation vectors approximates the tail vector. The goal of training is to maximize the score for triplets that actually occur in the graph and minimize it for triplets that don’t.
Today, a knowledge graph might include millions of entities and billions of relations between them. Embedding that much data would be impractical without parallelization.
In our paper, we consider three different parallel-computing settings: (1) multicore machines, with multiple CPUs; (2) GPU machines, with multiple CPUs and multiple GPUs; and (3) computing clusters, in which the training process is broken up across machines.
In each of these settings, DGL-KE organizes data storage and access differently. In multicore training, the complete knowledge graph is stored in main memory; in GPU training, entities are stored in main memory, but relations are stored in GPU memory; and in distributed training, the knowledge graph is divided up across machines, with a key-value database (KVStore, in the figure below) managing data accesses.
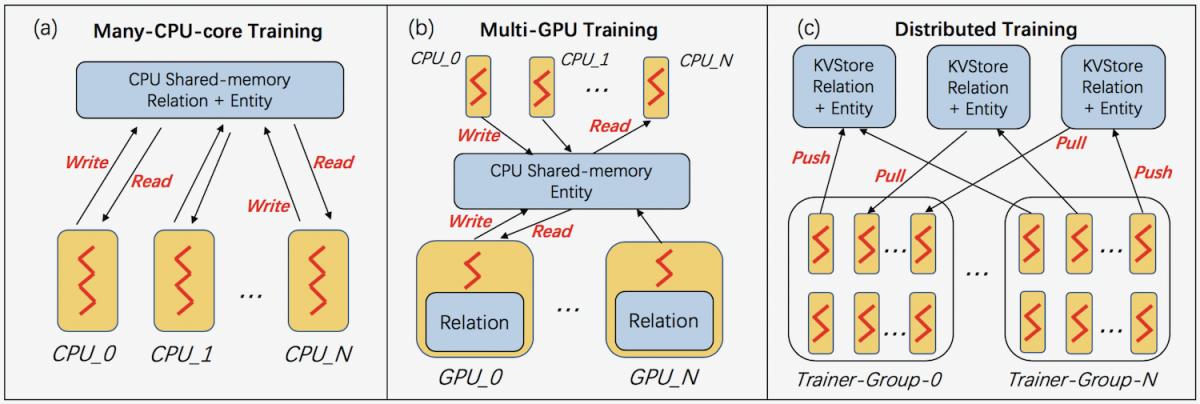
DGL-KE applies different optimizations in different settings, but they all share the goal, typical of parallel-computing schemes, of minimizing communication between parallel computing resources and storing data close to the processes that will use it.
The optimizations include
1. Graph partitioning: This optimization is specific to distributed training (training across multiple machines). To split the graph up for distribution across machines, we use METIS, a software suite that implements a minimum-cut algorithm. Minimum-cut is the problem of finding the smallest number of edge deletions that will divide a graph into two parts. By minimizing the number of edges linking chunks of the graph assigned to different machines, we reduce the need for communication between machines. METIS was developed by the academic lab of our team leader, Amazon senior principal scientist George Karypis, who is also a professor of computer science at the University of Minnesota.
2. Negative sampling: For each valid triplet extracted from the knowledge graph, we artificially create multiple negative examples — typically around 200 — by substituting spurious entities for its head or tail. This is computationally costly, because retrieving the spurious substitutions requires multiple calls to main memory. To reduce that cost, we use the same set of substitute entities for each valid triplet in a group. If the group has 100 members, this reduces the number of substitute entities we have to retrieve by 99%.
3. Relation partitioning: This optimization applies to both distributed training and multiple-GPU training, but it’s particularly important in the second case. To minimize communication overhead, we attempt to assign all relations of a particular type to only one GPU. We make this assignment iteratively, in a greedy fashion. At each iteration, we assign the most common relation type remaining to the GPU with the most available memory. This approach does reduce the randomness in the training procedure, which could make the resulting model less accurate. But we avoid that consequence by ensuring different distributions of the relations during each training epoch. (Knowledge-graph-embedding models, like most machine learning models, are trained multiple times on the same data set; each pass through the data is an epoch.)
4. Overlapping computations: In the GPU machines, CPUs have two tasks: assigning batches of training data to GPUs and updating the embeddings stored in main memory. The GPUs have one task: processing their batches of training data to compute the gradients that the CPUs will use to update the embeddings. To maximize efficiency, we keep both CPUs and GPUs busy by overlapping these computations. While the CPUs are updating embeddings based on one batch of data, the GPUs have already begun computing gradients for the next batch.
In experiments, we compared a distributed-training scheme using our optimizations to two existing training schemes, using five different methods for scoring embeddings during training. On average, our method yielded a twofold speedup relative to one baseline and a fivefold speedup relative to the other.

















