Secure multiparty computation (MPC) is a computing paradigm in which multiple parties compute an aggregate function — say, their average salary — without revealing any private information — say, their individual salaries — to each other. It’s found applications in auction design, cryptography, data analytics, digital-wallet security, and blockchain computation, among other things.

In 2023, the Association for Computing Machinery’s annual Dijkstra Prize in Distributed Computing was awarded to three papers on secure MPC from the late 1980s. One of those papers, “Verifiable secret sharing and multiparty protocols with honest majority”, grew out of the doctoral dissertation of Tal Rabin, a senior principal scientist in Amazon Web Services’ cryptography group and a professor of computer science at the University of Pennsylvania. She’s joined on the paper by her thesis advisor, Michael Ben-Or, a professor of computer science at the Hebrew University of Jerusalem, where Rabin earned her PhD.
In a remarkable twist, Rabin’s father, Michael Rabin, also won the Dijkstra Prize, in 2015, making the Rabins the only parent-child pair to have received the award. Even more remarkably, Michael Rabin’s co-recipient was one of his PhD students — Michael Ben-Or.
“So I am my father’s academic grandchild,” Rabin says.
Information-theoretic security
The field of secure MPC got off the ground in 1982, when Andrew Yao, now a professor of computer science at Tsinghua University, published a paper on secure two-party computation. The security of Yao’s MPC scheme, however, depended on the difficulty of factoring large integers — the same computational assumption that ensures the security of most online financial transactions today. Yao’s results immediately raised the question of whether secure MPC was possible even if an adversary had unbounded computational resources, a setting known as the information-theoretic (as opposed to computational) security setting.
The three 2023 recipients of the Dijkstra Prize all address the problem of information-theoretic secure MPC. The first two papers, both published at the 1988 ACM Symposium on Theory of Computing (STOC), prove that information-theoretic secure MPC is possible if no more than one-third of the participants in the computation are bad-faith actors who secretly share information and collusively manipulate their results.
Tal Rabin and Michael Ben-Or’s paper, which appeared at STOC the following year, improves that ratio to (approximately) one-half, which is provably the maximum number of defectors that can be tolerated in the information-theoretic setting. It’s also the threshold that Yao proved for his original computationally bounded approach.
Today, 35 years after Rabin and Ben-Or’s paper, techniques for information-theoretic secure MPC are beginning to find application. And as general-purpose quantum computers, which can efficiently factor large numbers, inch toward reality, information-theoretic — rather than computational — cryptographic methods become more urgent.
“The goal of our team is to apply MPC techniques to improve security and privacy at Amazon,” Rabin says.
Information checking
The heart of Rabin and Ben-Or’s paper is the adaptation of the concept of a digital signature to the information-theoretic setting. A digital signature is an application of public-key cryptography: The originator of a document has a private signing key and a public verification key, both derived from the prime factors of a very large number. Computing a document’s signature requires the private key, but verifying it requires only the public key. And an adversary can’t falsify the signature without computing the number’s factors.
Rabin and Ben-Or propose a method that they call information checking, which isn’t as powerful as digital signatures but makes no assumptions about defectors’ computational limitations. And it turns out to be an adequate basis for secure multiparty computation.
Rabin and Ben-Or’s protocol involves a dealer, an intermediary, and a recipient. The dealer has some data item, s, which it passes to the intermediary, who, at a later time, may in turn pass it to the recipient.
To mimic the security guarantees of digital signatures, information checking must meet two criteria: (1) if the dealer and recipient are honest, the recipient will always accept s if it is legitimate and will, with high probability, reject any fraudulent substitutions; and (2) whether or not the dealer is honest, the intermediary can predict with high probability whether or not the recipient will accept s. Together, these two criteria establish that fraudulent substitutions can be detected if either the dealer or the intermediary (but not both) is dishonest.
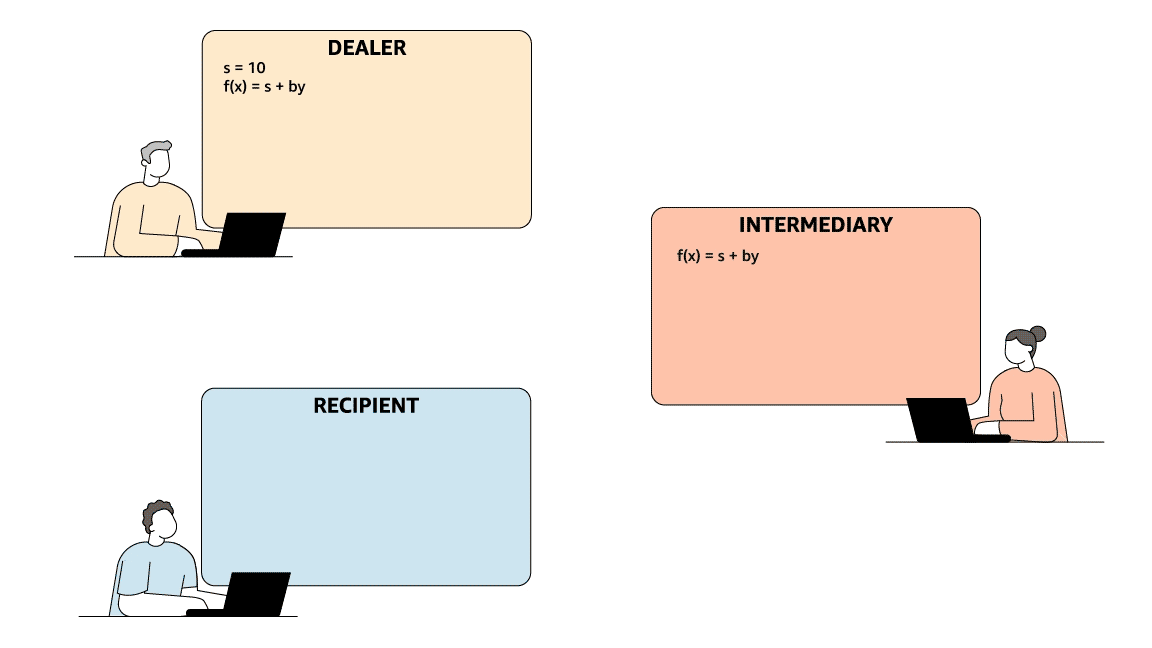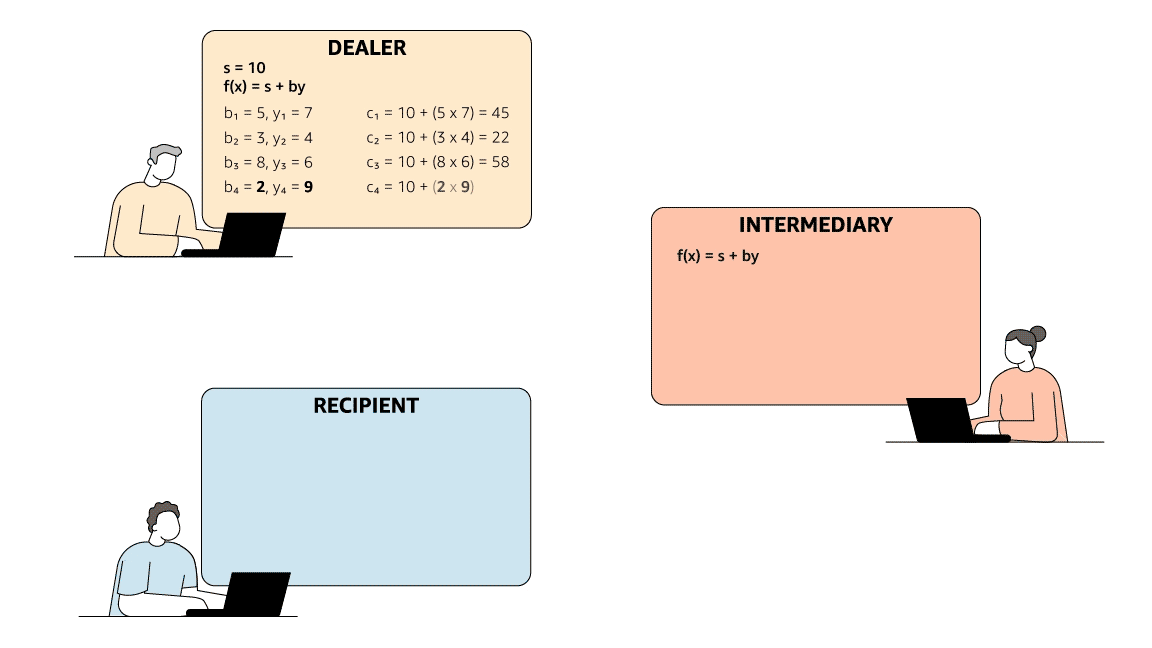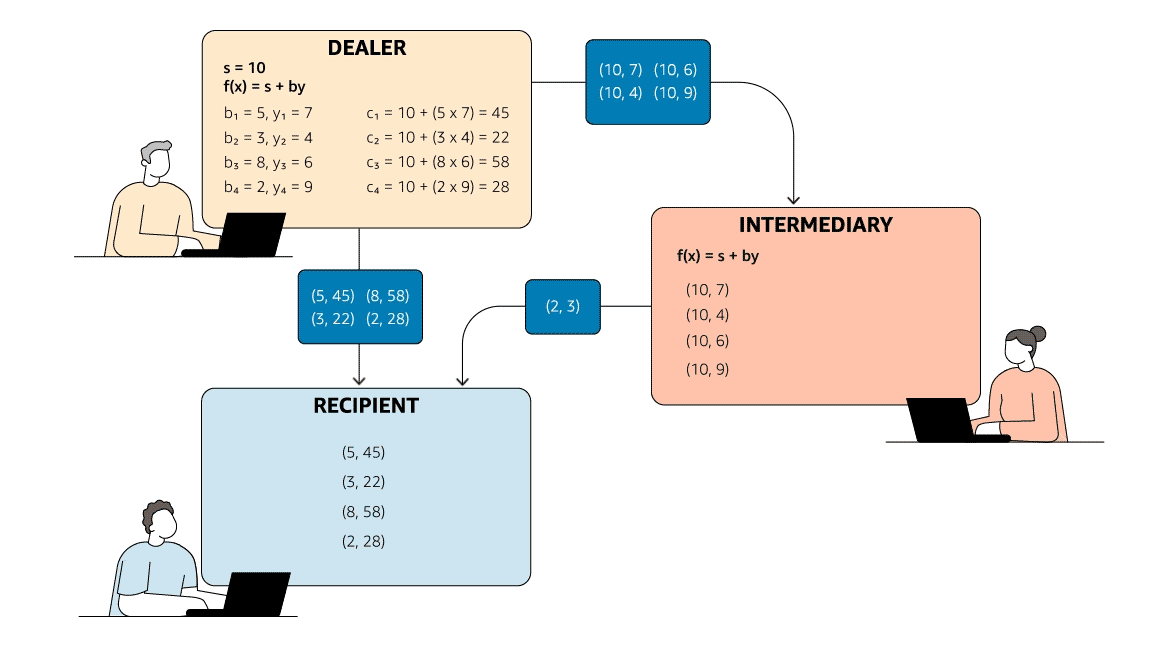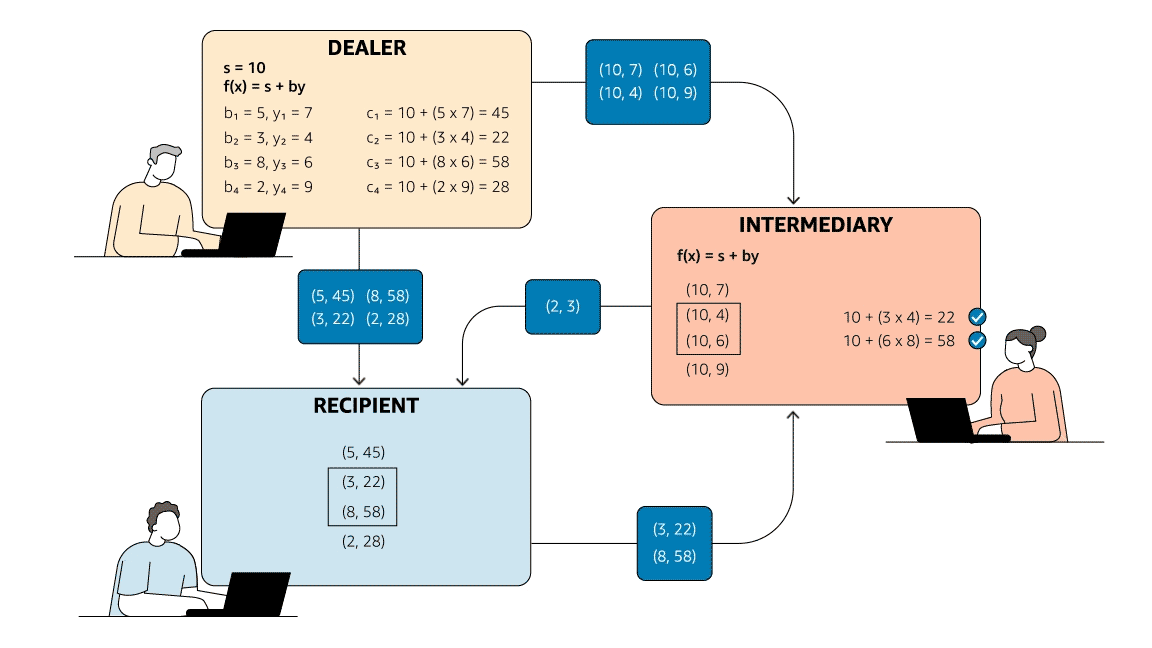
To meet the first criterion, the dealer sends the intermediary two values, s and a second number, y. It sends the recipient a different random number pair, (b, c), which satisfy an arithmetic operation (say, y = bs + c). The intermediary knows y and s but neither c nor b; if it attempts to pass the receiver a false s, the arithmetic operation will fail.
Zero-knowledge proofs
To meet the second criterion, Rabin and Ben-Or used a zero-knowledge proof, a mechanism that enables a party to prove that it knows some value without disclosing the value itself. Instead of applying an arithmetic operation to s and a single set of randomly generated numbers, the dealer applies it to s and multiple sets of randomly generated numbers, producing a number of (bi, ci) pairs. After the dealer has sent those pairs to the recipient, the intermediary selects half of them at random and asks the recipient to disclose them.
Since the intermediary knows s, it can determine whether the arithmetic relationship holds and, thus, whether the dealer has sent the recipient valid (bi, ci) pairs. On the other hand, since the intermediary doesn’t know the undisclosed pairs, it can’t, if it’s dishonest, game the system by trying to pass the recipient false y’s along with false s’s.
From weak to verifiable secret sharing
Next, Rabin and Ben-Or generalize this result to the situation in which there are multiple recipients, each receiving its own si. In this context, the authors show that their protocol enables weak secret sharing, meaning that if the recipients are trying to collectively reconstruct a value from their respective si’s, either they’ll reconstruct the correct value, or the computation will fail.
Providing a basis for secure MPC, however, requires the stronger standard of verifiable secret sharing, meaning that no matter the interference, the recipients’ collective reconstruction will succeed. The second major contribution made by Rabin and Ben-Or’s paper is a method for leveraging weak secret sharing to enable verifiable secret sharing.
In Rabin and Ben-Or’s protocol, all the (bi, ci) pairs sent to all the recipients are generated using the same polynomial function. In the multiple-recipient setting, the degree of the polynomial — its largest exponent — is half the number of recipients. To establish that a secret has been correctly shared, the dealer needs to show that all the received pairs fit the polynomial — without disclosing the polynomial itself. Again, the mechanism is a zero-knowledge proof.
“What we want is for parties to commit to their values via the weak secret sharing,” Rabin explains. “So now you know it's either one value or nothing. And then the dealer, on these values, proves that they all sit on a polynomial of degree T. Once that proof is done, you know about the values shared with weak secret sharing that they'll either be opened or not opened. You know that everything that is opened is on the same polynomial of degree T. And now you know you can reconstruct.”
When Rabin and Ben-Or published their paper, MPC research was in its infancy. “You can do information checking much better, much more efficiently and so on, today,” Rabin says. But the paper’s central result was theoretical. Today, designers of secure-MPC protocols can use any proof mechanism they choose, and they’ll enjoy the same guarantees on computability and defection tolerance that Rabin and Ben-Or established 35 years ago.