The Annual Conference on Quantum Information Processing (QIP) — the major conference in the quantum information field — was held this week, and Amazon Web Services is its sole diamond sponsor.
Two Caltech professors who are also members of the AWS Center for Quantum Computing — Amazon Scholar John Preskill and Fernando Brandão, the director of quantum applications for Amazon’s Quantum Computing group — are coauthors on six papers at QIP (see sidebar).
Additional QIP papers from members of the AWS Center for Quantum Computing
Center members’ names in bold.
"Provably efficient machine learning for quantum many-body problems"
Hsin-Yuan Huang, Richard Kueng, Giacomo Torlai, Victor V. Albert, and John Preskill
"Provably accurate simulation of gauge theories and bosonic systems"
Yu Tong, Victor Albert, Jarrod McClean, John Preskill, and Yuan Su
"Concentration for Trotter error"
Chi-Fang Chen and Fernando Brandão
"Fast Thermalization from the Eigenstate Thermalization Hypothesis"
Chi-Fang Chen and Fernando Brandão
"Random quantum circuits transform local noise into global white noise"
Alexander Dalzell, Nicholas Hunter-Jones and Fernando Brandão
But one of those — “Foundations for learning from noisy quantum experiments” — originated within Amazon’s Quantum Computing group, as did another QIP paper, “A randomized quantum algorithm for statistical phase estimation”.
“A randomized quantum algorithm for statistical phase estimation” describes a new method for statistical phase estimation, which could be used to calculate the ground-state energy of a molecule simulated by a quantum computer, among other applications. The technique requires fewer quantum bits (or qubits) to represent the molecule than existing methods do, and it also makes do with fewer gate operations, or manipulations of the quantum system.
“Foundations for learning from noisy quantum experiments” considers the case of a black-box quantum system — such as a noisy quantum computer — and shows that, if the system permits a particular set of quantum operations to be performed on it, its internal relationships can be accurately characterized. This means that near-term quantum computers with noisy qubits — that is, quantum computers that don’t always do what they’re supposed to — can still perform useful computations, because their operators can determine how noise is affecting the computational results.
Quantum computers
Where a bit in a classical computer can represent either 1 or 0, a qubit can represent 1, 0, or a quantum superposition of both. Perform a measurement on a qubit, however, and it falls out of superposition: it assumes a definite value, either 1 or 0.
If a group of qubits are entangled, so that their quantum properties depend on each other, then they can all share a single superposition. That superposition can be described as a probability distribution over definite states of the qubit array — states in which each qubit is either a 1 or a 0.
The probability distribution, in turn, is defined by a wave function, which has all the properties that electromagnetic waves do. When a sequence of measurements causes all the qubits to snap into definite states, the wave function is said to collapse.
Quantum computation consists of applying a series of operations — called gates, on the model of logic gates in classical computers — to an array of entangled qubits. For instance, a Hadamard gate puts a single qubit into superposition; a swap gate swaps two qubits.
The operations modify the qubits’ wave function so that it encodes some mathematical problem. When the wave function collapses, the definite values of the qubits represent — with high probability — the solution to the problem.
But maintaining entanglement across large numbers of qubits long enough to perform a useful computation is extremely difficult. To date, the largest quantum computer to exhibit entanglement has about 30 qubits. And most current qubits are “noisy”, or error prone.
Both the Amazon papers at QIP have a range of applications, but they’re well suited to the problem of near-term quantum computation, on devices with either limited numbers of qubits or noisy qubits.
Phase estimation
In 1994, when the world first learned of Peter Shor’s quantum algorithm for factoring numbers, it seemed that quantum computers might be able to solve an important class of problems — NP-complete problems — exponentially faster than classical computers.
Now, that seems unlikely. But one thing quantum computers definitely will do better than classical computers is simulate quantum systems.
For instance, simulations can help chemists, materials scientists, and drug developers better understand the molecules they’re working with. But accurate simulation requires the modeling of quantum interactions between atoms, which would be much more efficient on a quantum computer than it is on today’s classical computers.
Molecular simulation is the problem addressed in “A randomized quantum algorithm for statistical phase estimation”. The first author on the paper is Kianna Wan, a graduate student at Stanford University who was an intern at Amazon when the work was done. She’s joined by Mario Berta, a senior research scientist in the AWS Quantum Computing group, and Earl Campbell, who was also an Amazon senior research scientist at the time.
When a molecule is simulated on a quantum computer, the phase of the qubits’ wave function can be used to compute the molecule’s ground-state energy. But because measurements on the qubits cause the wave function to collapse, estimating the energy requires a series of measurements, which repeatedly sample the wave function’s probability distribution.
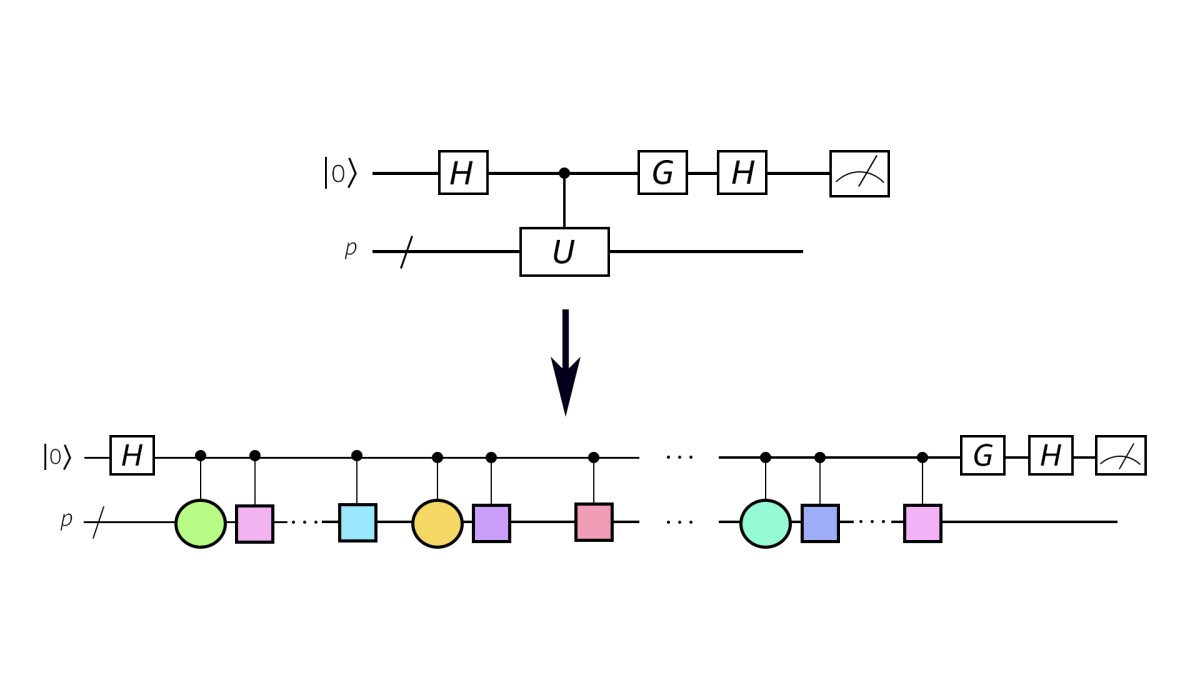
The number of qubits required to represent a molecule on a quantum computer is proportional to the size of the molecule. But existing methods of phase estimation require ancillary qubits — perhaps ten times the number of qubits required to represent the molecule — to encode the Hamiltonian matrix that represents the molecule’s energy function.
The Amazon researchers’ method allows more direct measurement of the qubits, because it uses importance sampling to preferentially sample the molecule’s strongest atomic interactions — the ones that contribute most to its overall energy.
This approach could end up requiring more samples than existing approaches. But given how hard qubits are to realize, in the near term, representing a molecule with, say, 100 qubits, and sampling those qubits more frequently, may be preferable to representing the molecule with 1,000 qubits and requiring fewer samples.
Learning from quantum experiments
In “Foundations for learning from noisy quantum experiments”, the researchers — first author Hsin-Yuan Huang, a Caltech graduate student who was an Amazon intern at the time; Steve Flammia, a principal research scientist at Amazon; and John Preskill, who’s Huang’s thesis advisor — consider a black-box quantum system: the experimenter can perform operations on the system and make measurements but otherwise has no idea how the system is internally configured.
In fact, the experimenter doesn’t know what effect the operations have on the system, nor what the measurements are measuring! Nonetheless, the authors prove a theorem stating that, if there exist operations that, in principle, allow the physical system to explore the full quantum Hilbert space — such as Hadamard gates and Toffoli gates — then it is possible to accurately characterize the system, including its noise properties.
The theorem is general: it could be useful for physical research on quantum-mechanical phenomena as well as quantum computing. But it has a clear application in the case of near-term quantum computers with noisy qubits. An accurate characterization of a noisy quantum computer could enable operators to devise experiments that yield useful results even given a certain probability of error.
Huang, Flammia, and Preskill also describe a pair of specific applications of their theory. The first is the use of neural networks to learn the characteristics of a quantum system.
They don’t use neural networks in the conventional way, however. Instead of simply providing sample inputs and outputs and letting the network learn correspondences between the two, they use the separate layers of the network to model consecutive operations applied to the quantum system and their results.
Within that formalism, however, they can use existing machine learning algorithms — gradient descent and backpropagation — to train the network. In a forthcoming paper, they show that, so long as the noise of the quantum system is below some threshold, this approach will yield a rigorous model of the system.
They also consider the case in which the qubits of a quantum computer are so noisy that rigorously characterizing them is impossible. Even in that case, they show, it’s possible to characterize the system well enough that on some computations, it can still afford speedups relative to classical computers.