In scientific and business endeavors, we are often interested in the causal effect of a treatment — say, changing the font of a web page — on a response variable — say, how long visitors spend on the page. Often, the treatment is binary: the page is in one font or the other. But sometimes it’s continuous. For instance, a soft drink manufacturer might want to test a range of possibilities for adding lemon flavoring to a new drink.
Typically, confounding factors exist that influence both the treatment and the response variable, and causal estimation has to account for them. While methods for handling confounders have been well studied when treatments are binary, causal inference with continuous treatments is far more challenging and largely understudied.
At this year’s International Conference on Machine Learning (ICML), my colleagues and I presented a paper proposing a new way to estimate the effects of continuously varied treatment, one that uses an end-to-end machine learning model in combination with the concepts of propensity score weighting and entropy balancing.
We compare our method to four predecessors — including conventional entropy balancing — on two different synthetic datasets, one in which the relationship between the intervention and the response variable is linear, and one in which it is nonlinear. On the linear dataset, our method reduces the root-mean-square error by 27% versus the best-performing predecessor, while on the nonlinear dataset, the improvement is 38%.
Propensity scores
Continuous treatments make causal inference more difficult primarily because they induce uncountably many potential outcomes per unit (e.g., per subject), only one of which is observed for each unit and across units. For example, there is an infinite number of lemon-flavoring volumes between one milliliter and two, with a corresponding infinity of possible customer preferences. In the continuous-treatment setting, a causal-inference model maps a continuous input to a continuous output, or response curve.
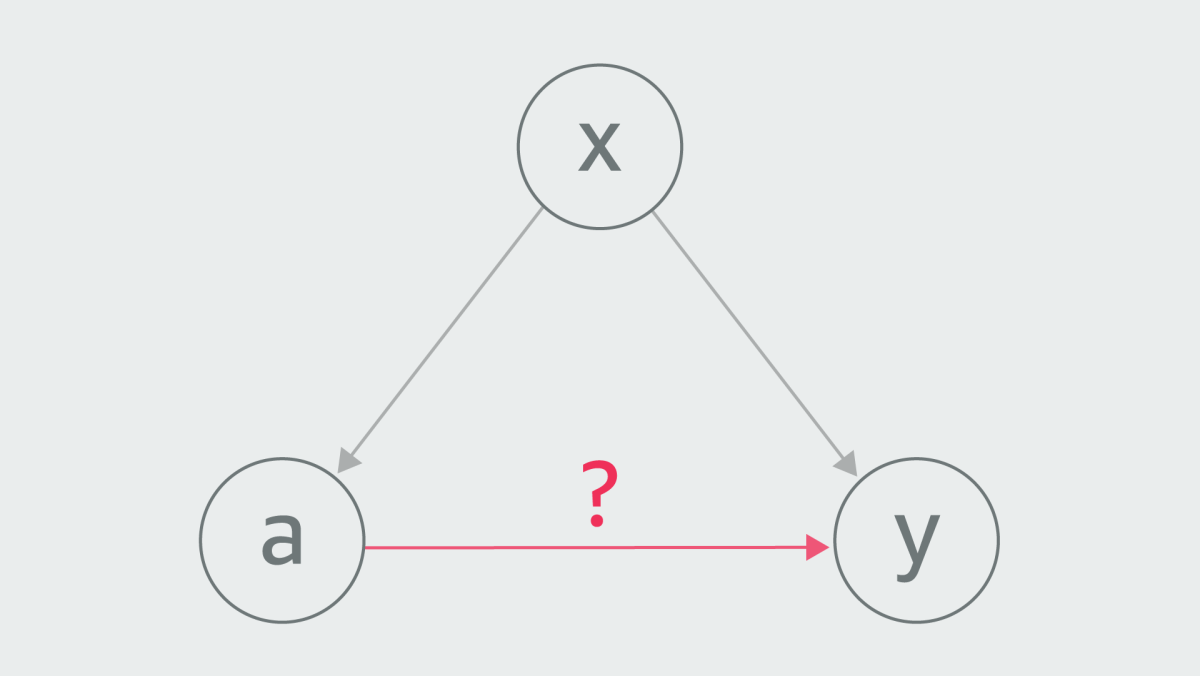
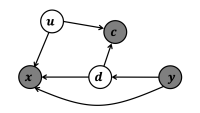
If two variables are influenced by a third — a confounder — it can be difficult to determine the causal relationship between them. Consider a simple causal graph, involving a treatment, a, a response variable, y, and a confounder, x, which influences both a and y.
In the context of continuous treatments, the standard way to account for confounders is through propensity score weighting. Essentially, propensity score weighting discounts the effect of one variable on another if they are both influenced by a confounder.
In our example graph, for instance, we would weight the edge between a and y according to the inverse probability of agiven x. That is, the greater the likelihood of a given x, the less influence we take a to have on y.
However, propensity scores can be very large for some units, causing data imbalances and leading to unstable estimation and uncertain inference. Entropy balancing is a way to rectify this problem, by selecting weights so as to minimize the differences between them — that is, maximize their entropy.
End-to-end balancing
Our new algorithm is based on entropy balancing and learns weights to directly maximize causal-inference accuracy through end-to-end optimization. We call end-to-end balancing, or E2B.
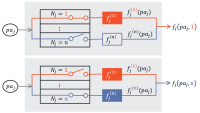
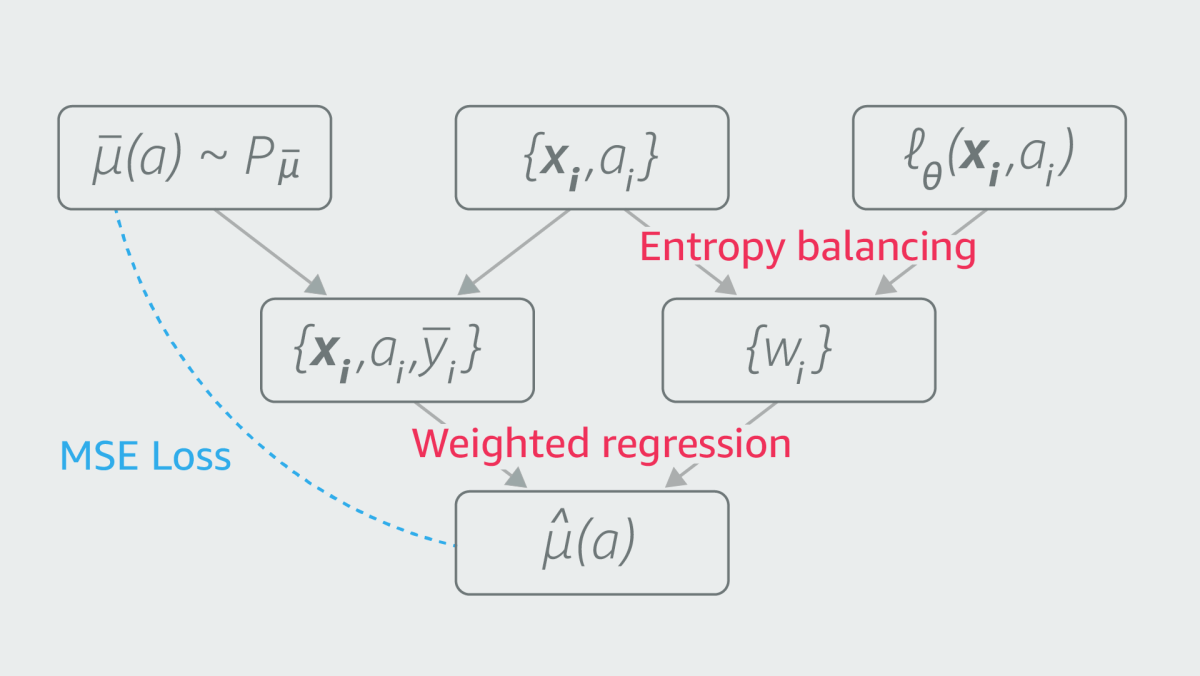
The figure below illustrates our approach. The variables {xi, ai} are pairs of confounders and treatments in the dataset, and lq is a neural network that learns to generate a set of entropy-balanced weights, {wi}, given a confounder-treatment pair. The function µ-bar (µ with a line over it) is a randomly selected response function — that is, a function that computes a value for a response variable (ȳ) given a treatment (a).
The triplets {xi, ai, ȳi} thus constitute a synthetic dataset: real x’s and a’s but synthetically generated y’s. During training, the neural network learns to produce entropy-balancing weights that re-create the known response function µ-bar. Then, once the network is trained, we apply it to the true dataset — with the real y’s — to estimate the true response function, µ-hat.
In our paper, we provide a theoretical analysis demonstrating the consistency of our approach. We also study the impact of mis-specification in the synthetic data generation process. That is, we show that even the initial selection of a highly inaccurate random response function — µ-bar — does not prevent the model from converging on a good estimation of the real response function, µ-hat.