Pretrained language models (PLMs) like BERT, RoBERTa, and DeBERTa, when fine-tuned on task-specific data, have demonstrated exceptional performance across a diverse array of natural-language tasks, including natural-language inference, sentiment classification, and question answering.
PLMs typically comprise a matrix for token embeddings, a deep neural network featuring an attention mechanism, and an output layer. The token-embedding matrix often constitutes a substantial portion of the model due to its extensive vocabulary table: for instance, it accounts for more than 21% of BERT’s model size and 31.2% of RoBERTa’s. Moreover, due to variances in token frequencies, the token-embedding matrix contains numerous redundancies. Thus, any technique capable of compressing the token embedding matrix has the potential to complement other methods for model compression, resulting in a heightened compression ratio.
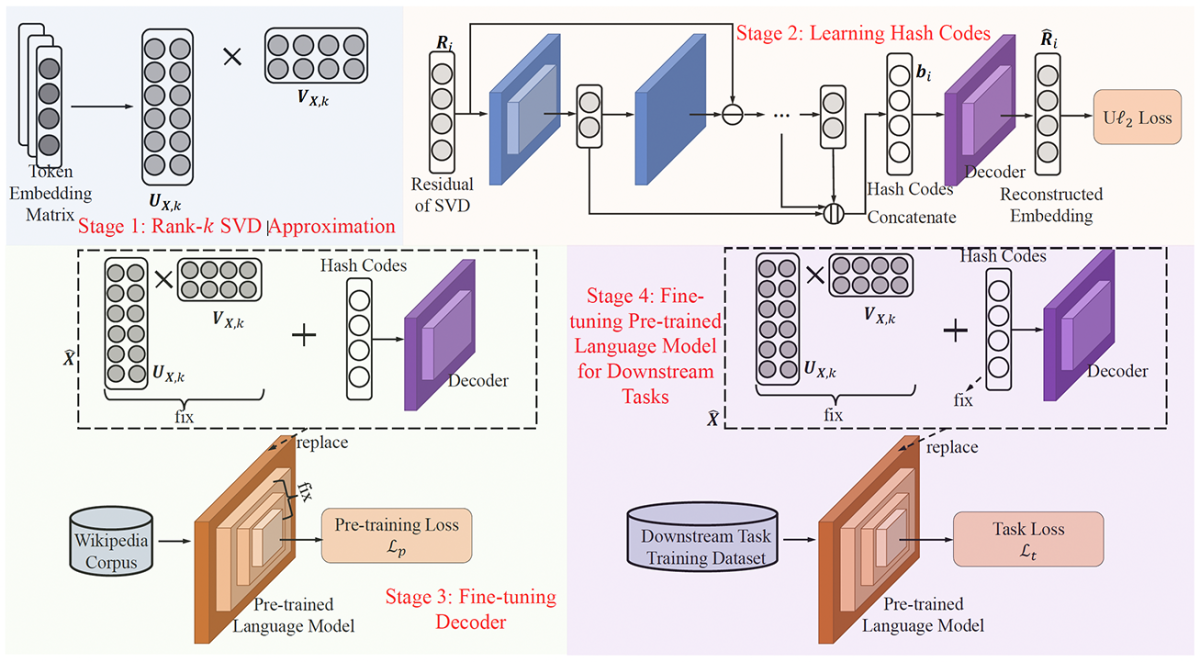
At this year’s Conference on Knowledge Discovery and Data Mining (KDD), my colleagues and I presented a new method for compressing token-embedding matrices for PLMs, which combines low-rank approximation, a novel residual binary autoencoder, and a fresh compression loss function.
We evaluated our method, which we call LightToken, on tasks involving natural-language comprehension and question answering. We found that its token-embedding compression ratio — the ratio of the size of the uncompressed matrix to that of the compressed matrix — was 25, while its best-performing predecessor achieved a ratio of only 5. At the same time, LightToken actually improved accuracy relative to existing matrix-compressing approaches, outperforming them by 11% on the GLUE benchmark and 5% on SQuAD v1.1.
Desiderata
The ideal approach to compressing token-embedding matrices for PLMs should have the following characteristics: (1) task agnosticity, to ensure effective application across diverse downstream tasks; (2) model agnosticity, allowing seamless integration as a modular component for various backbone models; (3) synergistic compatibility with other model compression techniques; and (4) a substantial compression ratio with little diminishment of model performance.
LightToken meets these criteria, generating compressed token embeddings in a manner that is independent of both specific tasks and specific models.
Rank-k SVD approximation
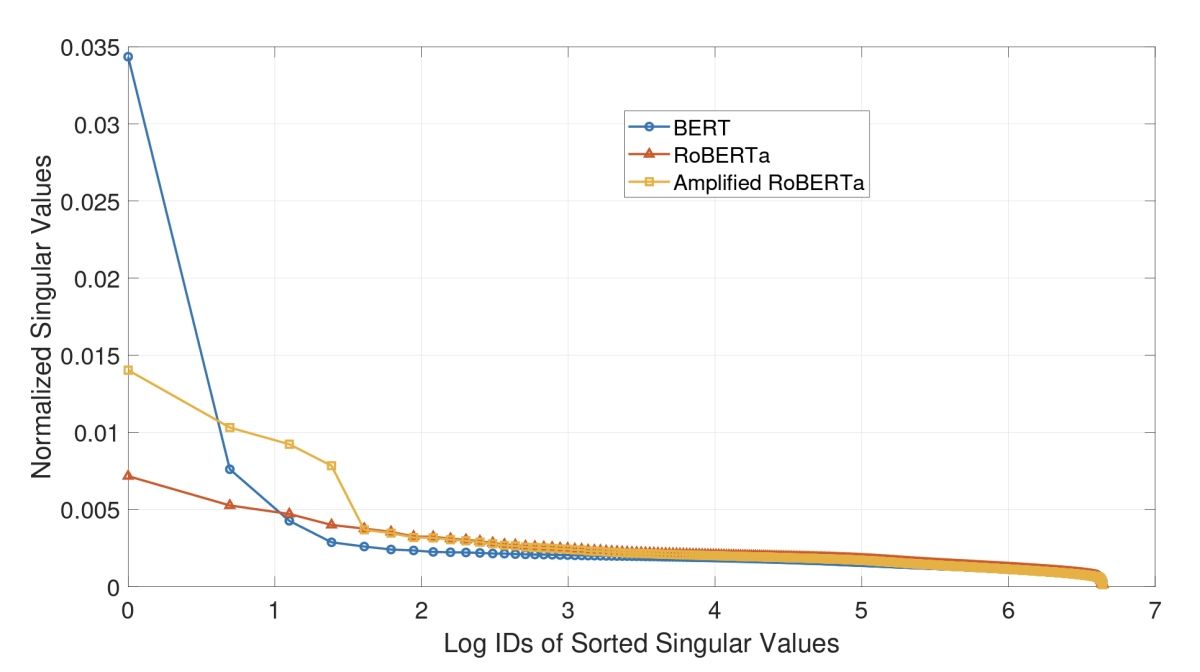
Numerous prior studies have highlighted the potency of singular-value decomposition (SVD) in effectively compressing model weight matrices. SVD decomposes a matrix into three matrices, one of which is a diagonal matrix. The entries in the diagonal matrix — the singular values — indicate how much variance in the data each variable explains. By keeping only the high singular values, it’s possible to project high-dimensional data down to a lower-dimensional subspace.
Token embedding matrices typically have a relatively small number of singular values. Consequently, the first step in our approach involves employing SVD to achieve a rank-𝑘 approximation for the token embedding matrix, for a small 𝑘.
Residual hashing
In experiments, we found that relying solely on the rank-k compression matrix, while it provided substantial compression, compromised performance on downstream tasks too severely. So LightToken also uses a residual binary autoencoder to encode the differences between the full token-embedding matrix and the matrix reconstituted from the rank-k compression matrix.

Autoencoders are trained to output the same values they take as inputs, but in between, they produce compressed vector representations of the inputs. We constrain those representations to be binary: they are the hash codes.
Binary codes are non-differentiable, however, so during model training, in order to use the standard gradient descent learning algorithm, we have to approximate the binary values with tempered sigmoid activation functions, which have a steep slope between low and high values.
Over multiple training epochs, however, tempered sigmoids have a tendency to saturate: every node in the network fires with every input, preventing the network from learning nonlinear functions. So we created a novel training strategy, in which the autoencoder is trained to a point short of saturation, and then it’s trained on the residual between the old residual and the new hash code. The final hash code is in fact a concatenation of hash codes, each of which encodes the residual of the previous code.
Loss function
Typically, a model like ours would be trained to minimize the Euclidean distance between the reconstructed token-embedding matrix and the uncompressed matrix. But we find that Euclidean distance yields poor performance on some natural-language-processing (NLP) tasks and on tasks with small training sets. We hypothesize that this is because Euclidean distance pays inadequate attention to the angle between vectors in the embedding space, which on NLP tasks can carry semantic information.
So we propose a fresh reconstruction loss, which serves as an upper limit for Euclidean distance. This loss encourages the model to prioritize alignment between the original and compressed embeddings by recalibrating cosine similarity.
We carried out comprehensive experiments on two benchmark datasets: GLUE and SQuAD 1.1. The outcomes clearly demonstrate the remarkable superiority of LightToken over the established baselines. Specifically, LightToken achieves an impressive 25-fold compression ratio while maintaining accuracy levels. Moreover, as the compression ratio escalates to 103, the incurred accuracy loss remains within a modest 6% deviation from the original benchmark.