Microphone arrays like the ones in Echo devices are being widely investigated as a way to enable sound source localization. Sound reaches the separate microphones of the array at different times, and the differences can be used to calculate the direction of the sound’s source.

In a paper presented at this year’s European Signal Processing Conference, we investigate the possibility of using fast transient sounds, such as hand claps and finger snaps, to identify a user’s location relative to a device equipped with a microphone array.
We propose a system that leverages the array to distinguish true control signals from environmental noise, such as fans, laughter, and background speech, and from “impulse interference” signals, such as a door shutting or a dropped cup hitting the floor.
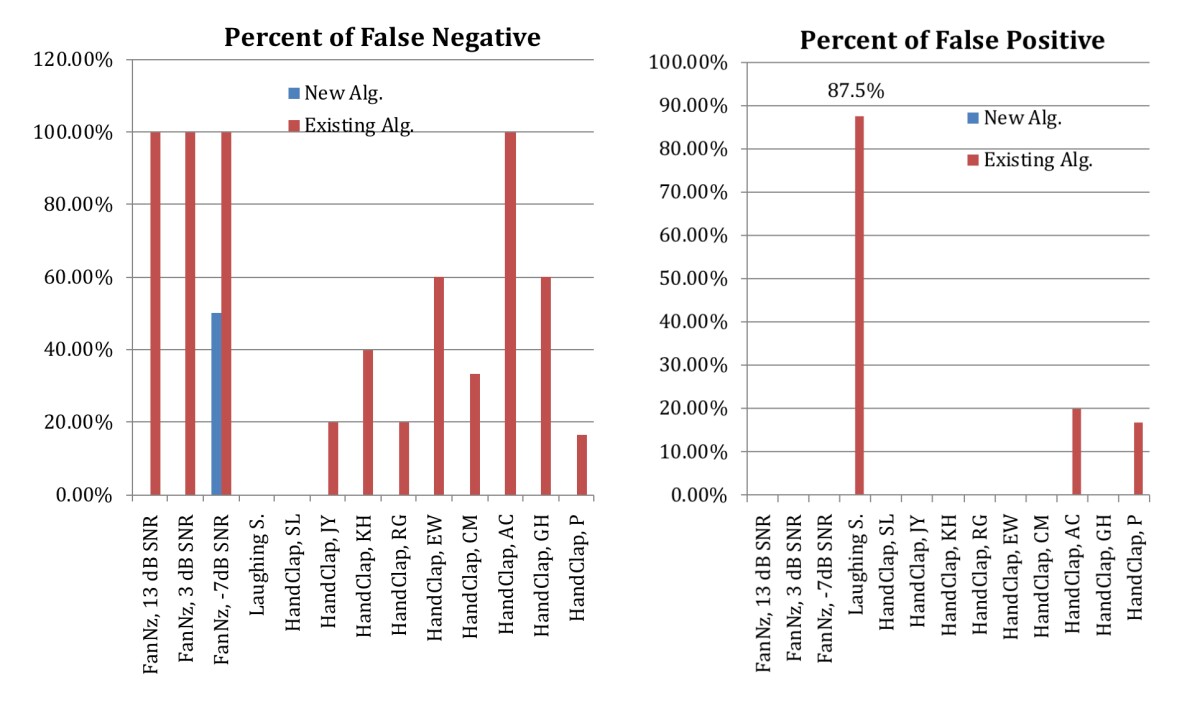
Existing algorithms for doing fast-transient-sound detection (FTSD) are both expensive in terms of computational complexity and susceptible to noise. They are also trained separately for minimization of false-positive and false-negative rates and for sound source localization, so it’s difficult to optimize the trade-offs between the two.
In our paper, “Dynamics and Periodicity Based Multirate Fast Transient-Sound Detection”, we describe a new algorithm that uses machine learning and data from a microphone array to overcome both of these problems. We also demonstrate that, on the basis of our FTSD algorithm, our detection algorithm for double fast-transient sounds (DFTSes), such as two claps or finger taps in succession, provides an optimal control mechanism.
To improve the accuracy of our FTSD analysis, we process the signal from each microphone in the array separately. Each microphone’s output passes through an FTSD module, and if the majority of the FTSD outputs are “true”, the system concludes that the input is a true control signal.
That assessment is based primarily on two signal characteristics: dynamics and periodicity. Dynamics is the difference between the signal’s highest and lowest power levels. Periodicity describes the signal’s tendency to repeat at regular intervals, as vowel sounds do in speech. Claps and slaps are nonperiodic, so if the input signal exhibits periodicity, the system should disregard it.
The first thing our algorithm does is to downsample the input signal, twice. Voice services sample sound at a high rate — say, between 32 and 96 kilohertz (kHz), or 32,000 to 96,000 samples per second. To gauge dynamics, however, 16 kHz is adequate, and 2 kHz is enough to determine periodicity. Reducing the sampling rate makes the computation much more efficient.
The 16 kHz and 2 kHz audio signals are processed in parallel. First, both signals pass through linear predictors, which analyze sequences of signal segments and attempt to predict future segments. The predicted signals are then subtracted from the actual measured signals. The result is a pair of modified signals called linear-prediction-error signals, in which noise is reduced.
The error signals pass to modules that analyze dynamics and periodicity. The dynamics module determines whether spikes in the input signal are sharp enough to indicate sounds of interest, such as claps and snaps; that threshold is something our system learns from training data. To determine periodicity, we use a technique called autocorrelation, in which different time segments of the signal are aligned and compared. If the signal is periodic, the segments will look similar. Again, the relevant degree of similarity is something the system learns.
Our FTSD algorithm performs these analyses in parallel on the signals received from all the microphones in the array. A nonperiodic signal that exceeds the dynamics threshold counts as a yes vote. If the signals of more than half the microphones yield yes votes, the algorithm judges the signal spike to indicate an acoustic event of interest.
If the FTSD algorithm outputs true votes for two consecutive signal spikes, our system estimates the time delays between all the 16 kHz error signals. If all the time-delay-estimation (TDE) values are in a predefined range, our DFTS detection (DFTSD) algorithm outputs a judgement of true, because DFTSes of interest should happen closely in location and closely in time.
Both our theoretical analyses and objective test results show that our system offers significant improvement in FTSD, DFTSD, and SSL.
Acknowledgements: Philip Hilmes and Carlo Murgia




