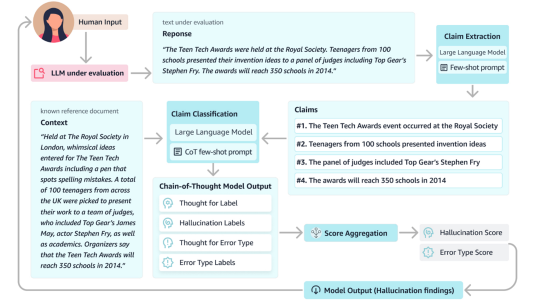
Many of today’s most useful AI systems are multilabel classifiers: they map input data into multiple categories at once. An object recognizer, for instance, might classify a given image as containing sky, sea, and boats but not desert or clouds.
Earlier this month, at the International Conference on Machine Learning, my colleagues and I presented a new approach to doing computationally efficient multilabel classification. In tests, we compared our approach to four leading alternatives using three different data sets. On five different performance measures, our system demonstrated improvements across the board.
The need for multilabel classification arises in many different contexts. Originally, it was investigated as a means of doing text classification: a single news article, for instance, might touch on multiple topics. Since then, it’s been used for everything from predicting protein function from raw sequence data to classifying audio files by genre.
The challenge of multilabel classification is to capture dependencies between different labels. If an image features sea, for instance, it’s much more likely to also feature boats than an image that features desert. In principle, the way to capture such dependencies is to learn a joint probability, which represents the likelihood of any combination of probabilities for all labels.
In practice, calculating an accurate joint probability for more than a handful of labels requires an impractically large amount of data. Two years ago, at NeurIPS, my colleagues and I demonstrated that using recurrent neural networks to chain single-label classifiers in sequence was a more computationally efficient way to capture label dependencies. Recurrent neural networks, or RNNs, process sequenced inputs in order, so that the output corresponding to any given input factors in the inputs and outputs that preceded it. RNNs thus automatically consider dependencies.
Our earlier paper, however, assumed that the order in which the classifiers are applied is fixed, regardless of context. Order matters because errors by classifiers early in the chain propagate through subsequent classifications. If the classifier chain erroneously labels an image as containing sea, for instance, it becomes more likely to mislabel it as containing boats.
The way to combat this problem is to move more error-prone classifiers later in the chain. But a given classifier’s propensity for error is relative to its inputs: some classifiers are very reliable for certain types of data but unreliable for others.
Our new approach is to train a system to dynamically vary the order in which the chained classifiers process the inputs, according to features of the input data. This ensures that the classifiers that are most error prone relative to a particular input move to the back of the chain.
In our experiments, we explored two different techniques for doing this. Our first technique used an RNN to generate a sequence of labels for a particular input. Then we excised the erroneous labels while preserving the order of the correct ones. If the resulting sequence omitted any correct labels, we appended them at the end in a random order. This new sequence then became a target output, which we used to re-train the RNN on the same input data.
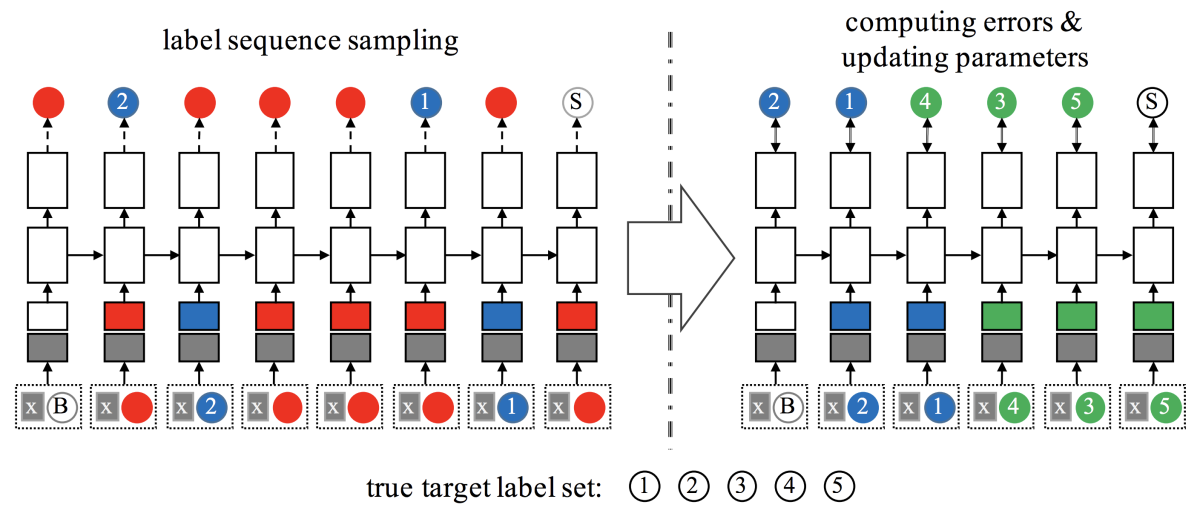
By preserving the order of the correct labels, we ensure that classifiers later in the chain learn to take advantage of classifications earlier in the chain. Initially, the output of the RNN is entirely random, but it eventually learns to tailor its label sequences to the input data. Note that while the training data is annotated to indicate the true labels, it is not annotated to indicate the ideal sequence of classifications. Hence the need for us to generate new training targets on the fly.
Reinforcement learning is the second technique we used to train an RNN to do dynamic classifier chaining. In reinforcement learning, a machine learning system learns a “policy,” which consists of a set of actions to take under different circumstances. It learns the policy through trial and error, gauging its success according to a “reward function”, which measures how far a selected action takes it toward some predefined goal.
In our case, the actions were simply the applications of labels to the input data, and the reward function measured the accuracy of the classification that resulted from the chain of classifiers.
In tests, we compared our systems to four different baselines. Each adopted a different strategy for determining classifier order. Two chained classifiers according to how common their labels were, the third used an arbitrary but fixed ordering, and the fourth generated a separate arbitrary ordering for each input.
We used five different metrics to evaluate system performance. One considered only the accuracy of the single most probable label, two the accuracies of the three most probable labels, and two the accuracies of the five most probable labels. For the three-label and five-label cases, we used two different evaluation strategies. One measured overall accuracy across labels, while the other assigned greater value to accurate assessments of the first few labels.
Our best-performing system combined the outputs of our two dynamic-chaining algorithms to produce a composite classification. On each of the five metrics, and on three different data sets, that combination outperformed whichever of the four baselines offered the best performance, usually by about 2% to 3% and in one instance by nearly 5%.