In the absence of a vaccine, a valuable measure for controlling the spread of COVID-19 is large-scale testing. The limited availability of test kits, however, means that testing has to be done as efficiently as possible.
The most efficient testing protocol is group testing, in which test samples from multiple subjects are tested together. If the test is perfectly reliable, then a negative test for a group clears all of its members at once. Clever group selection enables the protocol to zero in on infected patients with fewer tests than would be required to test each patient individually.
Group testing is a well-studied problem, but particular aspects of COVID testing — among them the relatively low infection rate among the test population, the false-positive rate of the tests, and practical limits on the number of samples that can be pooled in a single group — mean that generic test strategies dictated by existing theory are suboptimal.
My colleagues and I have written a paper that presents optimal strategies for COVID testing in several different circumstances. The paper is currently under submission for publication, but we have posted it to arXiv in the hope that our ideas can help stimulate further advances in COVID test design.
The key to group testing is that a given test sample is tested in several different groups, each of which combines it with a different assortment of samples. By cross-referencing the results of all the group tests, it’s possible to predict with high probability the correct result for any given sample.
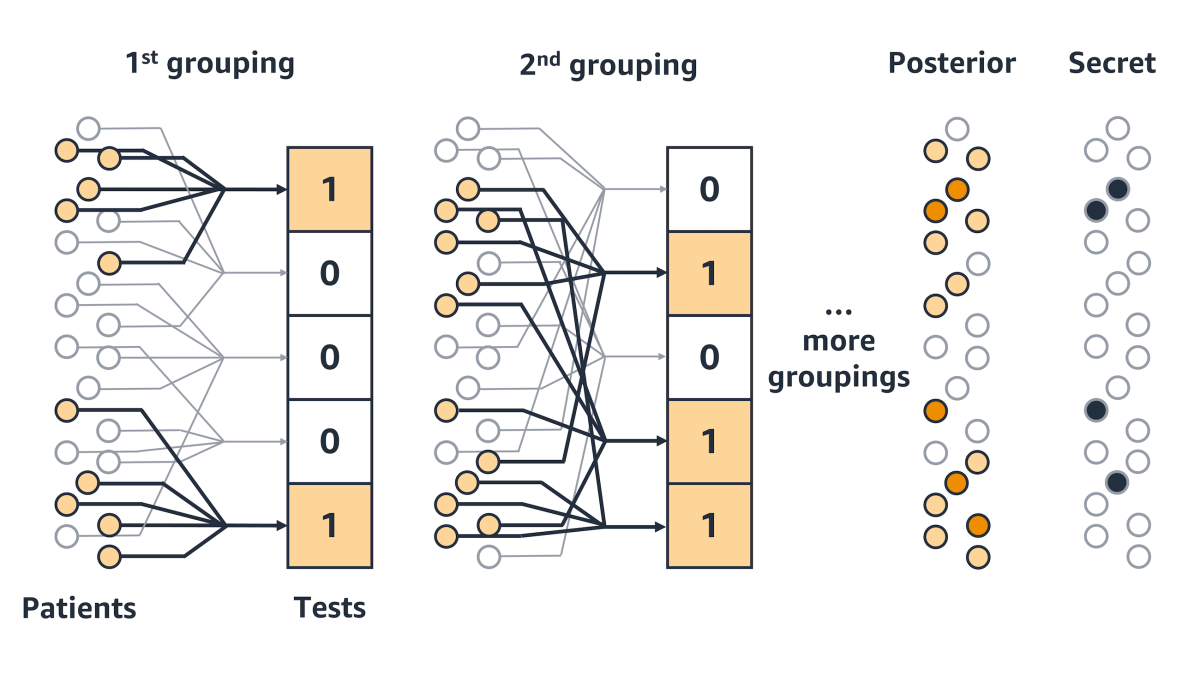
In this respect, the problem exactly reproduces the classical problem of error-correcting codes in information theory. Each parity bit in an error-correcting code encodes information about several message bits, and by iteratively cross-referencing message bits and parity bits, it’s possible to determine whether errors have crept into either.
Accordingly, we treat the problem of deciding how to pool test samples as a coding problem, and the problem of interpreting the test results as a decoding problem, and we use the information-theoretic concept of information gain to evaluate test protocols.
Adaptive testing
Group testing comes in two varieties: adaptive and non-adaptive. In the adaptive setting, tests (or groups of tests) are conducted in sequence, and the outcomes of one round of testing inform the group selection for the next round. In non-adaptive testing, groups are selected without any prior information about group outcomes.
In our paper, we consider adaptive testing involving relatively small numbers of patients — less than 30. We also consider non-adaptive testing for much larger numbers — say, thousands. In both settings, using the tools of information theory, we factor in prior knowledge about the probability of infection — some patients’ risk is higher than others’ — and the false-positive and false-negative rates of the tests.
Even with small numbers of patients, given the uncertainty of the test results and the mixture of prior infection probabilities, calculating the optimal composition of the test groups is an intractably complex problem. We show that in the COVID-19 setting, evolutionary strategies offer the best approximation of the optimal composition.
With evolutionary strategies, test groups are assembled at random, and the likely information gain is computed (given the prior probability of a positive test for each patient). Then some of the group compositions are randomly varied and tested again. Variations that lead to greater information are explored further; those that don’t are abandoned.
This procedure will produce the best approximation of the optimal group composition, but it could take a while: there’s no theoretical guarantee about how quickly evolutionary strategies will converge on a solution. As an alternative in the context of adaptive testing with small numbers of patients, we also consider a greedy group composition strategy.
With the greedy strategy, we first assemble the group that, in itself, maximizes the information gain for one round of testing. Then we select the group that maximizes the information gain in the next round, and so on. In our paper, we show that this approach is very likely to arrive at a close approximation of the ideal group composition, with tighter guarantees on the convergence rate than evolutionary strategies offer.
Non-adaptive testing
For large-scale, non-adaptive tests, the conventional approach is to use Bloom filter pooling. The Bloom filter is a mechanism designed to track data passing through a network in a streaming, online context.
The Bloom filter uses several different hash functions to hash each data item it sees to several different locations in an array of fixed size. Later, if any location corresponding to a given data item is empty, the filter can guarantee that that item hasn’t been seen. False positives, however, are possible.
Group testing has appropriated this design, using the multiple hash functions to assign a single patient’s sample to multiple locations and grouping samples that hash to the same location. But no matter how good the hash functions are, the distribution across groups may not be entirely even. If the groups average, say, 20 members each, some might have 18, others 22, and so on. That compromises the accuracy of the ensuing predictions of infection.
The Bloom filter design assumes that the number of data items seen in the streaming, network setting is unpredictable and open ended. But in the group-testing context, we know exactly how many patient samples we’re distributing across groups. So we can exactly control the number of samples assigned to each group.
If we have no prior probabilities of infection rates, an even distribution is optimal. If we do have priors, then we can distribute samples accordingly: maximizing information gain might require that we reduce the sizes of groups containing high-probability samples and increase the sizes of groups containing low-probability samples.
Similarly, because the Bloom filter was designed for the streaming, networked setting, the algorithm for determining whether an item has been seen must be highly efficient; the trade-off is that it doesn’t minimize the risk of a false positive.
In the context of group testing, we can afford a more involved but accurate decoding algorithm. In our paper, we show that a message-passing algorithm, of a type commonly used to decode error-correcting codes, is much more effective than the standard Bloom filter decoding algorithm.




