In the past year, we’ve introduced what we call name-free skill interaction for Alexa. In countries where the service has rolled out, a customer who wants to, say, order a car can just say, “Alexa, get me a car”, instead of having to specify the name of a ride-sharing provider.
Underlying this service is a neural network that maps utterances to skills, and expanding the service to new skills means updating the network. The optimal way to do that would be to re-train the network from scratch, on all of its original training data, plus data corresponding to any new skills. If the network requires regular updates, however, this is impractical — and Alexa has added tens of thousands of new skills in the past year alone.
At this year’s meeting of the North American Chapter of the Association for Computational Linguistics, we present a way to effectively and efficiently update our system to accommodate new skills. Essentially, we freeze all the settings of the neural network and add a few new network nodes to accommodate the new skills, then train the added nodes on just the data pertaining to the new skills.
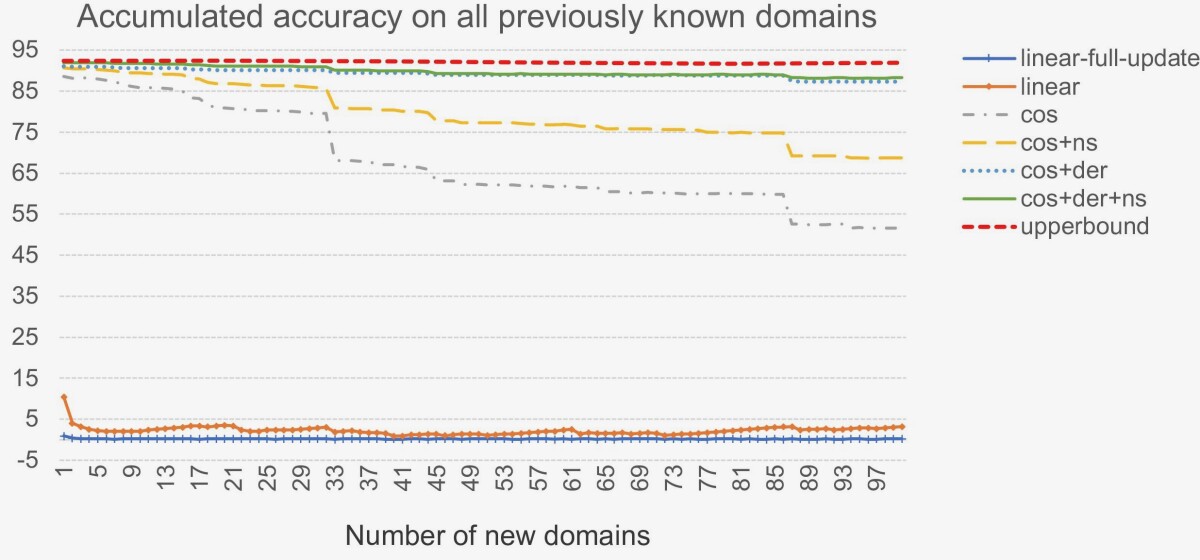
If this is done naively, however, the network’s performance on existing skills craters: in our experiments, its accuracy fell to less than 5%. With a few modifications to the network and the training mechanism, however, we were able to preserve an accuracy of 88% on 900 existing skills while achieving almost 96% accuracy on 100 new skills.
We described the basic architecture of our skill selection network — which we call Shortlister — in a paper we presented last year at the Association for Computational Linguistics’ annual conference.
Neural networks usually have multiple layers, each consisting of simple processing nodes. Connections between nodes have associated “weights”, which indicate how big a role one node’s output should play in the next node’s computation. Training a neural network is largely a matter of adjusting those weights.
Like most natural-language-understanding networks, ours relies on embeddings. An embedding represents a data item as a vector — a sequence of coordinates — of fixed size. The coordinates define points in a multidimensional space, and data items with similar properties are grouped near each other.
Shortlister has three modules. The first produces a vector representing the customer’s utterance. The second uses embeddings to represent all the skills that the customer has explicitly enabled — usually around 10. It then produces a single summary vector of the enabled skills, with some skills receiving extra emphasis, on the basis of the utterance vector.
Finally, the third module takes as input both the utterance vector and the skill summary vector and produces a shortlist of skills, ranked according to the likelihood that they should execute the customer’s request. (A second network, which we call HypRank, for hypothesis ranker, refines that list on the basis of finer-grained contextual information.)
Embeddings are typically produced by neural networks, which learn during training how best to group data. For efficiency, however, we store the skill embeddings in a large lookup table, and simply load the relevant embeddings at run time.
When we add a new skill to Shortlister, then, our first modification is to add a row to the embedding table. All the other embeddings remain the same; we do not re-train the embedding network as a whole.
Similarly, Shortlister’s output layer consists of a row of nodes, each of which corresponds to a single skill. For each skill we add, we extend that row by one node. Each added node is connected to all the nodes in the layer beneath it.
Next, we freeze the weights of all the connections in the network, except those of the output node corresponding to the new skill. Then we train the new embedding and the new output node on just the data corresponding to the new skill.
By itself, this approach leads to what computer scientists call “catastrophic forgetting”. The network can ensure strong performance on the new data by funneling almost all inputs toward the new skill.
In Shortlister’s third module — the classifier — we correct this problem by using cosine similarity, rather than dot product, to gauge vector similarity.
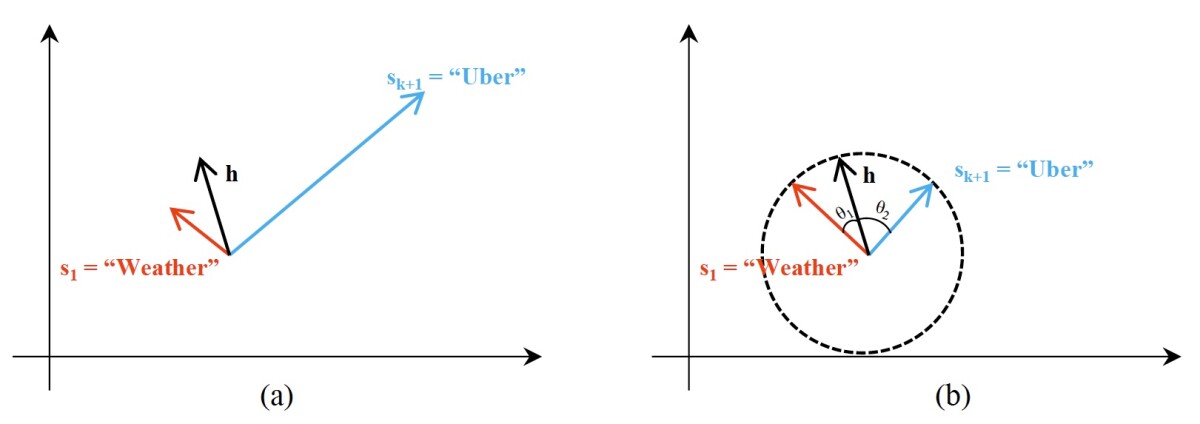
The classifier works by mapping inputs (customer utterances, combined with enabled-skill information) and outputs (skill assignments) to the same vector space and finding the output vector that best approximates the input vector. A vector can be thought of as a point in space, but it can also be thought of us a line segment stretching from the origin through that point.
Usually, neural networks use dot products to gauge vector similarity. Dot products compare vectors by both length and angle, and they’re very easy to calculate. The network’s training process essentially normalizes the lengths of the vectors, so that the dot product is mostly an indicator of angle
But when the network is re-trained on new data, the new vectors don’t go through this normalization process. As in the figure above, the re-trained network can ensure good performance on the new training data by simply making its vector longer than all the others. Using cosine similarity to compare vectors mitigates this problem.
Similarly, when the network learns the embedding for a new skill, it can improve performance by making the new skill’s vector longer than other skills’. We correct this problem by modifying the training mechanism. During training, the new skill’s embedding is evaluated not just on how well the network as a whole classifies the new data, but on how consistent it is with the existing embeddings.
We used one other technique to prevent catastrophic forgetting. In addition to re-training the network on data from the new skill, we also used small samples of data from each of the existing skills, chosen because they were most representative of their respective data sets.
In experiments, we first trained a network on 900 skills, then re-trained it, sequentially, on each of 100 new skills. We tested six versions of the network: two baselines that don’t use cosine similarity and four versions that implemented various combinations of our three modifications.
For comparison, we also evaluated a network that was trained entirely from scratch on both old and new skills. The naïve baselines exhibited catastrophic forgetting. The best-performing network used all three of our modifications, and its accuracy of 88% on existing skills was only 3.6% lower than that of the model re-trained from scratch.
Acknowledgments: Han Li, Jihwan Lee, Sidharth Mudgal, Ruhi Sarikaya

















