Reinforcement learning (RL) is an increasingly popular way to model sequential decision-making problems in artificial intelligence. RL agents learn through trial and error, repeatedly interacting with the world to learn a policy that maximizes a reward signal.
RL agents have recently achieved remarkable results when used in conjunction with deep neural networks. Chief among these so-called deep-RL results is the 2015 paper that introduced the Deep Q Network (DQN) agent, which surpassed human-level performance on a large set of Atari games.
A core component of DQN is an optimizer that adapts the parameters of the neural network to minimize the DQN objective. We typically use optimization algorithms that are standard in deep learning, but these algorithms were not designed to account for the intricacies that arise when solving deep RL.
At this year's Conference on Neural Information Processing Systems (NeurIPS), my coauthors and I presented a new optimizer that is better equipped to deal with the difficulties of RL. The optimizer makes use of a simple technique, called proximal updates, that enables us to hedge against noisy updates by ensuring that the weights of the neural network change smoothly and slowly. To achieve this, we steer the network toward its previous solution when there is no indication that doing so would harm the agent.
Tuning gravity
We show in the paper that the DQN agent could best be thought of as solving a series of optimization problems. At each iteration, the new optimization problem is based on the previous iterate, or the network weights that resulted from the last iteration. Also known as the target network in the deep-RL literature, the previous iterate is the solution we gravitate toward.
While the target network encodes the previous solution, a second network — called the online network in the literature — finds the new solution. This network is updated at each step by moving in the direction that minimizes the DQN objective.
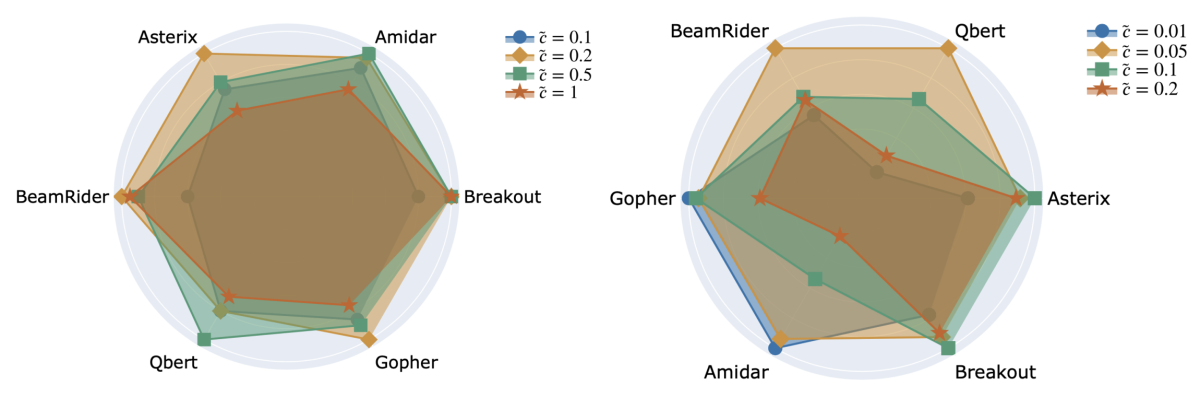
The gradient vector from minimizing the DQN objective needs to be large enough to cancel the default gravity toward the previous solution (the target network). If the online and target networks are close, the proximal update would behave similarly to the standard DQN update. But if the two networks are far apart, the proximal update can be significantly different from the DQN update, in that it would encourage closing the gap between the two networks. In our formulation, we can tune the degree of gravity exerted by the previous solution, with noisier updates requiring higher gravity.
While proximal updates lead to slower shifts in the neural-network parameters, they also lead to faster improvement at obtaining high rewards, the primary quantity of interest in RL. We show in our paper that this improvement applies to both the interim performance of the agent and its asymptotic. It also applies both in the context of planning with noise and in the context of learning on large-scale domains where the presence of noise is all but guaranteed.
Evaluation
To evaluate our approach in the learning setting, we added proximal updates to two standard RL algorithms: the DQN algorithm mentioned above and the more competitive Rainbow algorithm, which combines various existing algorithmic improvements in RL.
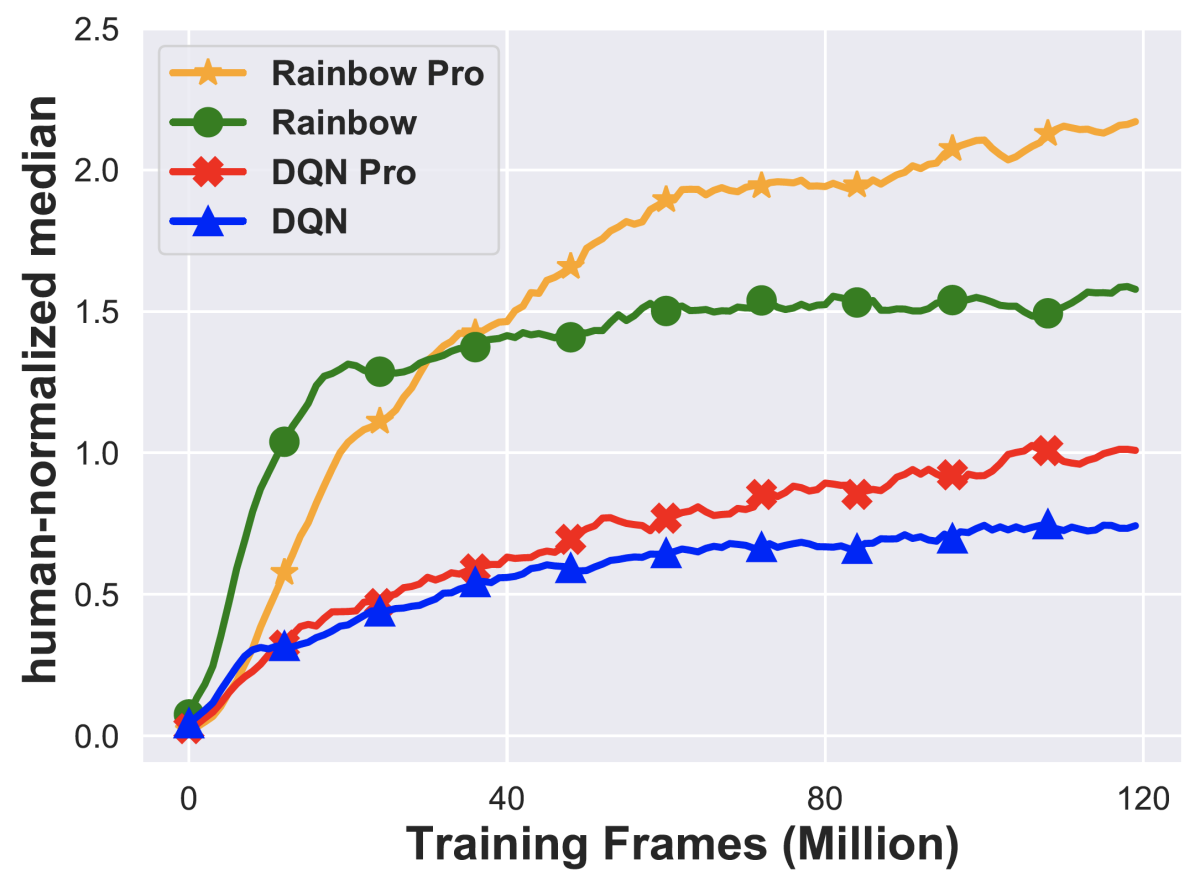
We then tested the new algorithms, called DQN with Proximal updates (or DQN Pro) and Rainbow Pro on a standard set of 55 Atari games. We can see from the graph of the results that (1) the Pro agents overperform their counterparts; (2) the basic DQN agent is able to obtain human-level performance after 120 million interactions with the environment (frames); and (3) Rainbow Pro achieves a 40% relative improvement over the original Rainbow agent.
Further, to ensure that proximal updates do in fact result in smoother and slower parameter changes, we measure the norm differences between consecutive DQN solutions. We expect the magnitude of our updates to be smaller when using proximal updates. In the graphs below, we confirm this expectation on the four different Atari games tested.
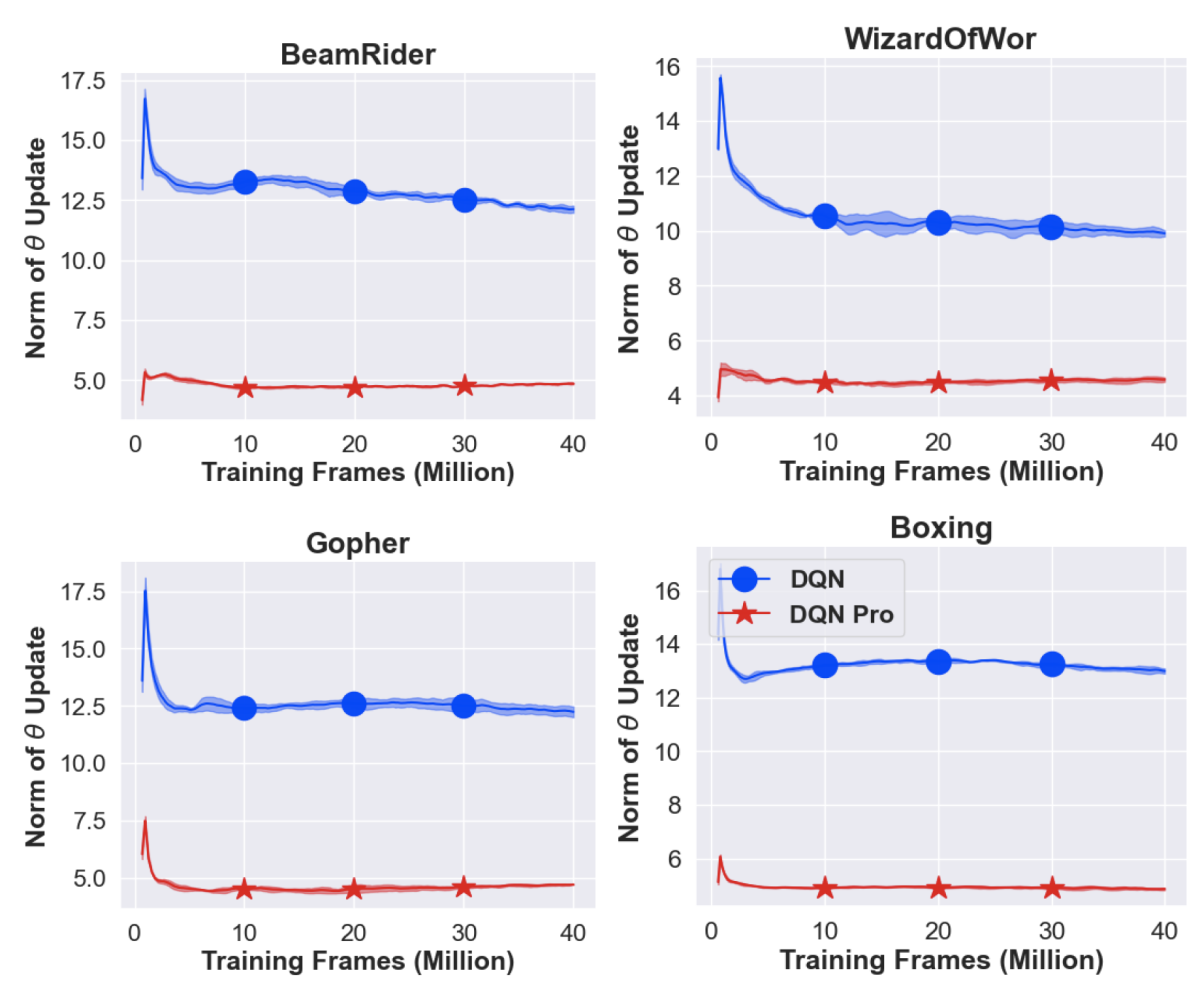
Overall, our empirical and theoretical results support the claim that when optimizing for a new solution in deep RL, it is beneficial for the optimizer to gravitate toward the previous solution. More importantly, we see that simple improvements in deep-RL optimization can lead to significant positive gains in the agent’s performance. We take this as evidence that further exploration of optimization algorithms in deep RL would be fruitful.
We have released the source code for our solution on GitHub.