Large machine learning models based on the transformer architecture have recently demonstrated extraordinary results on a range of vision and language tasks. But such large models are often too slow for real-time use, so practical systems frequently rely on knowledge distillation to distill large models’ knowledge into leaner, faster models.
The defining characteristic of the transformer model is its reliance on attention mechanisms, which determine the influence that previously seen data should have on the model’s handling of the data at hand. The attention mechanisms are typically organized into multiple heads, each of which attends to a different aspect of the data.
Typically, large-transformer distillation involves aligning the attention heads of the large, trained model — the teacher — with the attention heads of the leaner, target model — the student — on a one-to-one basis. But limiting the number of attention heads is one of the ways in which the student model can reduce model complexity.
At this year’s meeting of the Association for the Advancement of Artificial Intelligence (AAAI), we proposed an alternative, in which the knowledge of all the attention heads in the teacher model is distilled into all the attention heads of the student model. Since the student has fewer heads than the teacher, a single attention head in the student model may end up encoding information contained in several of the teacher’s attention heads.
We evaluated our approach on two different vision-language models, which map images and texts to the same vector space. The models had been fine-tuned on a visual-question-answering task, an image-captioning task, and a translation task based on image context, and we compared our distillation approach to two state-of-the-art baselines. Our approach outperformed the baselines across the board.
Target tasks
Typically, a vision-language model (VLM) has a separately pretrained sub-module for each of its modalities, and the whole network is then further pretrained to learn a multimodal representation. Finally, the pretrained model is then fine-tuned on a specific task.
In our experiments, we distilled the student model only on the fine-tuned task. We did, however, consider the case in which the teacher model did not have any multimodal pretraining and found that our distillation method could, to a great extent, compensate for that lack.
Weighting game
For a given input or set of inputs, each attention head of a transformer constructs an attention map, a matrix that indicates the influence that each element of the input exerts on each of the other elements. In an LLM, the attention map maps the words of a text sequence against themselves; when deciding on each new output word, the LLM uses the attention weights in the matrix column corresponding to that word. In a vision model, the map might represent the influence that each region of an image exerts on the interpretation of every other region.
The rows of any matrix can be concatenated to produce a single vector, and our approach to knowledge distillation relies on the vector versions — or “flattened” versions — of attention maps.
The loss function for the distillation process has two components. One is a function that seeks to minimize the difference between the teacher and student outputs; obviously, it’s crucial that the student reproduce the functionality of the teacher model as accurately as possible. The other component of the loss function aligns attention maps.
Specifically, for a given training example and a given attention head in the teacher model, the attention-map-alignment loss seeks to minimize the distance between the teacher’s attention map and a weighted sum of the maps generated by all the student attention heads.
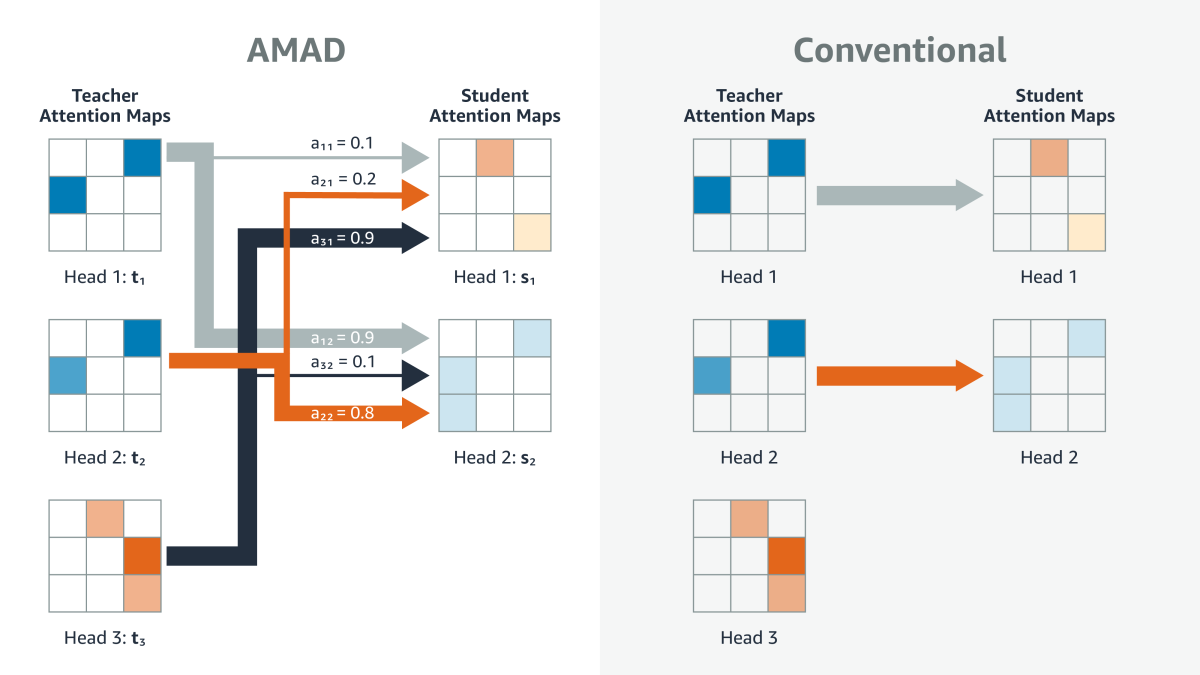
The weights of that weighted sum are based on the cosine similarities between the flattened teacher map and the flattened student maps. In other words, student maps that are already similar to the teacher map count more toward the weighted sum. Over successive steps of the training process, that similarity should increase, and so should the weights assigned to the similar student maps.
If the student had exactly the same number of attention heads as the teacher, and there were no correlations whatever between the maps generated by the teacher’s attention heads, this process might result in something similar to the one-to-one mapping of the standard distillation process. But of course, the point of the approach is to preserve attention map information even when the student has fewer attention heads than the teacher.
And empirically, there’s usually some correlation between attention maps generated by different heads. Indeed, those correlations may explain the success of our method; it’s because of them that multiple attention maps generated by the teacher can be distilled into a single map generated by the student.
Acknowledgments: Srikar Appalaraju, Peng Tang, Vijay Mahadevan, R. Manmatha, Ying Nian Wu.