Generative adversarial networks (GANs) are a technology that can produce remarkably realistic synthetic images. From a set of real images, a GAN learns a mapping from a latent distribution to the image distribution represented in the training dataset.
Modifying images by controlling GANs is a lively topic of research, whose applications include dataset creation and augmentation, image editing, and entertainment. Researchers have developed ever more sophisticated techniques for both exploring and structuring latent spaces, in order to understand how movement through the spaces translates to modification of synthetic images' properties.
In a paper that we presented at this year’s European Conference on Computer Vision (ECCV), my colleagues and I describe a new technique that offers precise control over GAN outputs. Unlike prior techniques, ours can hold selected image attributes steady — say, the location and appearance of one sofa in a room — while varying others.

Prior approaches to controlling GANs depended on linear trajectories through the latent space, along which some feature would vary — say, the age of the faces being generated, or the extent to which they were smiling or frowning. Researchers either looked for existing axes in a latent space, in which case the correlations with image features were rarely exact, or they intentionally structured the space so that it lent itself to linear trajectories, in which case they had to know in advance which image features they wanted to control.
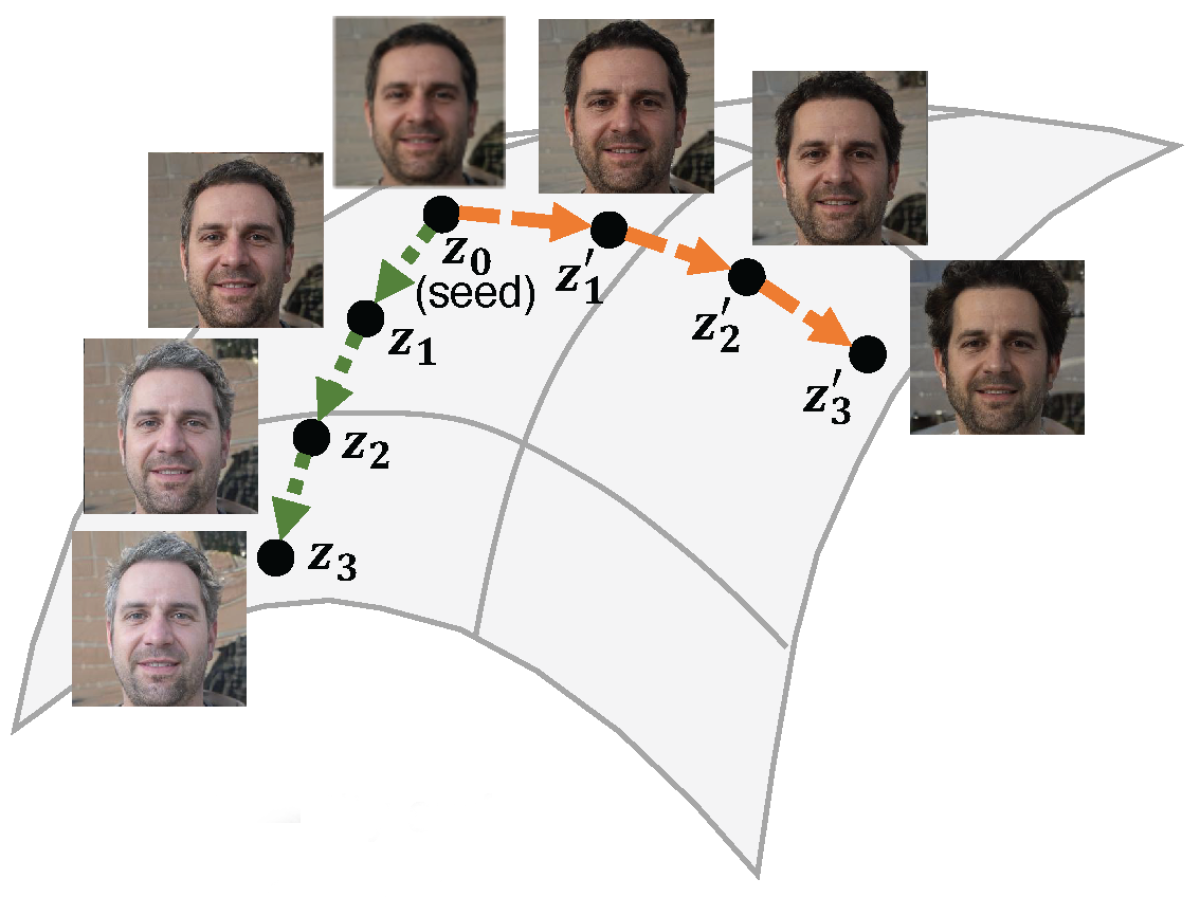
Instead of correlating spatial axes with predetermined features, our method plots a nonlinear trajectory through a GAN’s latent space. Consequently, it can work with existing GANs, regardless of the structure of their latent spaces. That means we can, in principle, control multiple arbitrary attributes.
By the same token, we can control features that would be difficult for humans to annotate accurately — and therefore difficult to capture by modifying the structure of the latent space. For instance, taking the Fourier transform of an image, we can fix the high-frequency characteristics and vary the low-frequency characteristics, producing clearly distinct images whose variations, however, are difficult to explain:

Finally, most work on controllable GANs has focused on synthetic faces, which simplifies the problem somewhat, since the same facial characteristics tend to inhabit approximately the same regions of the image. Our method, because it plots local trajectories through an arbitrary latent space, can handle more diverse types of images.
Rayleigh quotients
Our approach depends on the intuition that for any point within the latent space, there exist local trajectories in which desired attributes do not change. We treat the calculation of such a trajectory as an optimization problem — particularly, a Rayleigh quotient.
We assume that for any point in the latent space, there is a function that maps the corresponding image to some kind of feature set. In the case of features like hair length or eye color, the function would be a neural network, trained on the relevant classification tasks; in the case of high-frequency and low-frequency image characteristics, the function is a closed-form transformation like the Fourier transform.
The aim is to find a local trajectory through the latent space that minimizes variation in the outputs of some of those functions while maximizing variation in the outputs of others. Optimizing the ratio of those variations is an instance of Rayleigh quotient maximization.
We approximate relative displacements in the space using local linear expansions — linear approximations of a function’s value at a given point that are based on its derivatives. Assembling the matrix of derivatives — the Jacobian, which measures variation or rate of change along different dimensions — requires us to sample local points in the latent space. Once we’ve done that, the maximization of the Rayleigh quotient has a closed-form solution, which gives us the optimal trajectory through the space.
We traverse that trajectory for a short distance, then re-compute a new Rayleigh quotient. The distance between waypoints is a hyper-parameter of the method, which varies according to function. In our experiments, we chose parameters that led to small but perceptible differences in the images corresponding to the waypoints.
In those experiments, we compared our approach to three prior approaches that found linear trajectories within the latent space, using GANs trained on two different datasets, one a set of faces and one a set of living room scenes. We found that, across the board, our approach did a better job than the baselines of both fixing the features to be fixed and varying the features to be varied.