Neural networks have been responsible for most of the top-performing AI systems of the past decade, but they tend to be big, which means they tend to be slow. That’s a problem for systems like Alexa, which depend on neural networks to process spoken requests in real time.
In natural-language-understanding (NLU) applications, most of a neural network’s size comes from a huge lookup table that correlates input words with “embeddings.” An embedding is a large vector (usually a sequence of 300 numbers) that captures information about a word’s meaning.
In a paper that we and our colleagues are presenting at the 33rd conference of the Association for the Advancement of Artificial Intelligence (AAAI), we describe a new method for compressing embedding tables that compromises the NLU network’s performance less than competing methods do.
In one set of experiments, for instance, we showed that our system could shrink a neural network by 90 percent while reducing its accuracy by less than 1%. At the same compression rate, the best prior method reduced the accuracy by about 3.5%.
The ability to compress NLU models means that, as Alexa learns to perform more and more complex tasks, she can continue to deliver responses in milliseconds. It also means that Alexa’s skill base can continue to expand unfettered. Alexa currently supports more than 70,000 third-party skills, with thousands more being added every month. Compression means that those skills’ NLU models can be stored efficiently.
In our experiments, we used a set of pretrained word embeddings called Glove. Like other popular embeddings, Glove assesses words’ meanings on the basis of their co-occurrence with other words in huge bodies of training data. It then represents each word as a single point in a 300-dimensional space, such that words with similar meanings (similar co-occurrence profiles) are grouped together.
NLU systems often benefit from using such pretrained embeddings, because it lets them generalize across conceptually related terms. (It could, for instance, help a music service learn that the comparatively rare instruction “Play the track ‘Roadrunner’” should be handled the same way as the more common instruction “Play the song ‘Roadrunner”.) But it’s usually possible to improve performance still further by fine-tuning the embeddings on training data specific to the task the system is learning to perform.
In previous work, NLU researchers had taken a huge lookup table, which listed embeddings for about 100,000 words, reduced the dimension of the embeddings from 300 to about 30, and used the smaller embeddings as NLU system inputs.
We improve on this approach by integrating the embedding table into the neural network in such a way that it can use task-specific training data not only to fine-tune the embeddings but to customize the compression scheme as well.
To reduce the embeddings’ dimensionality, we use a technique called singular-value decomposition. Singular-value decomposition (SVD) produces a lower-dimensional projection of points in a higher-dimensional space, kind of the way a line drawing is a two-dimensional projection of objects in three-dimensional space.
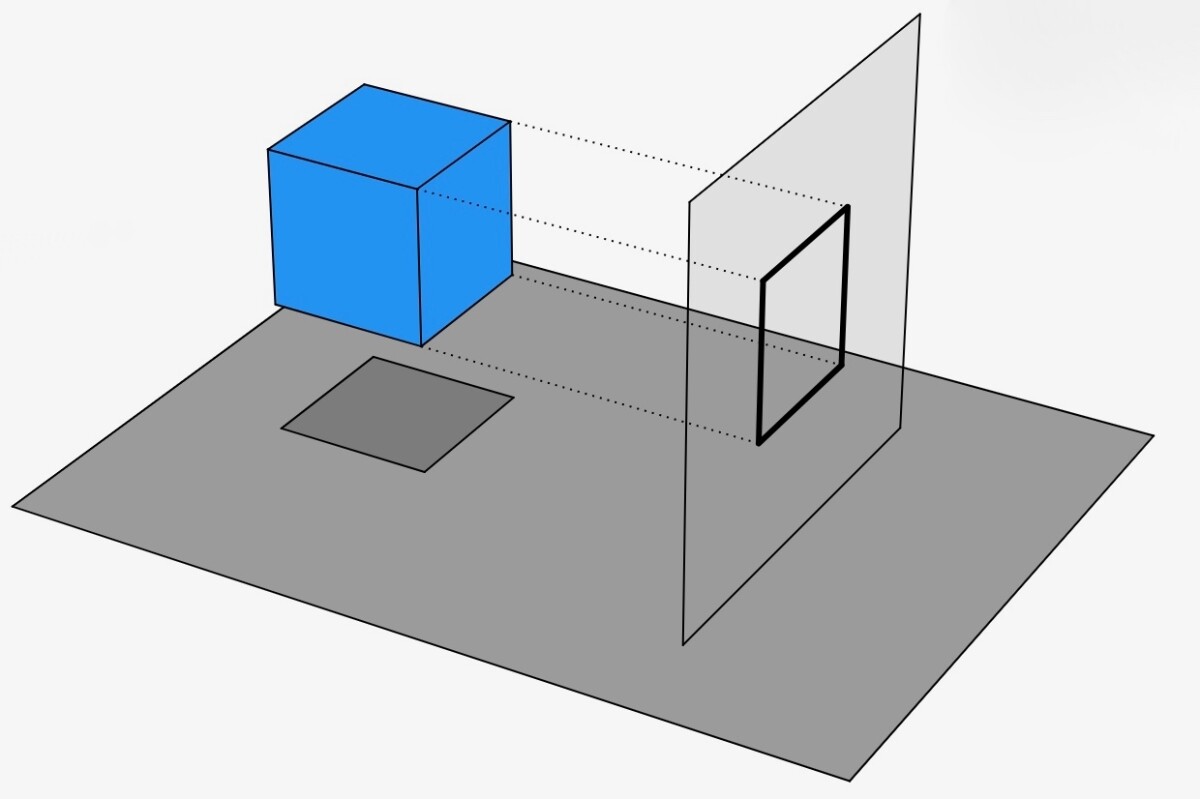
The key is to orient the lower-dimensional space so as to minimize the distance between the points and their projections. Imagine, for instance, trying to fit a two-dimensional plane to a banana so as to minimize the distance between the points on the banana’s surface and the plane. A plane oriented along the banana’s long axis would obviously work better than one that cut the banana in half at the middle. Of course, when you’re projecting 300-dimensional points onto a 30-dimensional surface the range of possible orientations is much greater.
We use SVD to break our initial embedding matrix into two smaller embedding matrices. Suppose you have a matrix that is 10,000 rows long (representing a lexicon of 10,000 words) and 300 columns wide (representing a 300-dimensional vector for each word). You can break it into two matrices, one of which is 10,000 columns long and 30 columns wide, and the other of which is 30 columns long and 300 columns wide. This results in a reduction of parameters, from 10,000 x 300 to ((10,000 x 30) + (30 x 300)), or almost 90%.
We represent one of these matrices as one layer of a neural network and the second matrix as the layer above it. Between the layers are connections that have associated “weights,” which determine how much influence the outputs of the lower layer have on the computations performed by the higher one. The training process keeps readjusting those weights, trying to find settings that reduce the projection distance still further.
In our paper, we also describe a new procedure for selecting the network’s “learning rate”. The relationship between the weight settings of the entire network and the network’s error rate can be imagined as a landscape with peaks and valleys. Each point in the landscape represents a group of weight settings, and its altitude represents the corresponding error rate.
The goal is to find a group of weights that correspond to the bottom of one of the deepest valleys, but we can’t view the landscape as a whole; all we can do is examine individual points. At each point, however, we can calculate the slope of the landscape, and the standard procedure for training a neural network is to continually examine points that lie in the downhill direction from the last point examined.
Every time you select a new point, the question is how far in the downhill direction to leap, a metric called the learning rate. A recent approach to choosing the learning rate is the cyclical learning rate, which steadily increases the leap length until it hits a maximum, then steadily steps back down to a minimum, then back up to the maximum, and so on, until further exploration no longer yields performance improvements.
We vary this procedure by decreasing the maximum leap distance at each cycle, then pumping it back up and decreasing it again. The idea is that the large leaps help you escape local minima — basins at the tops of mountains rather than true valleys. But tapering the maximum leap distance reduces the chance that when you’ve found a true valley and have started down its slope, you’ll inadvertently leap out of it.
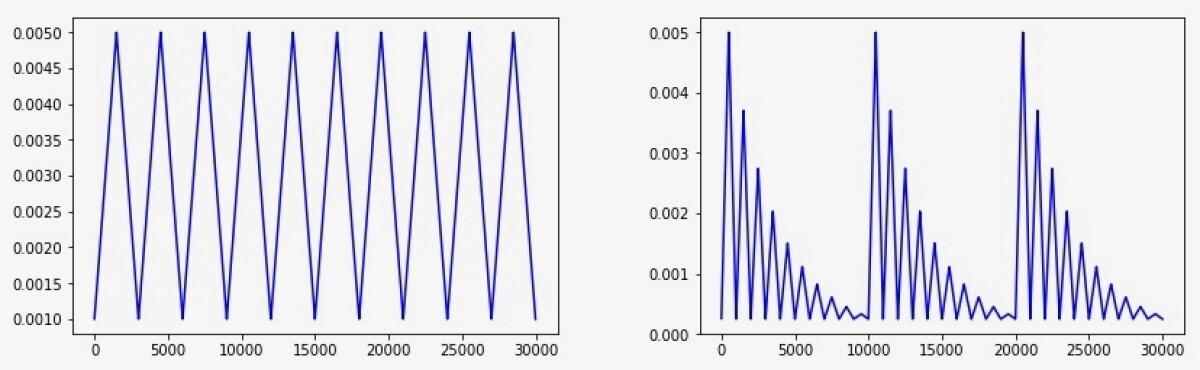
We call this technique the cyclically annealed learning rate, and in our experiments, we found that it led to better performance than either the cyclical learning rate or a fixed learning rate.
To evaluate our compression scheme, we compared it to two alternatives. One is the scheme we described before, in which the embedding table is compressed before network training begins. The other is simple quantization, in which all of the values in the embedding vector — in this case, 300 — are rounded to a limited number of reference values. So, for instance, the numbers 75, 83, and 87 might all become 80. This can reduce, say, 32-bit vector values to 16 or 8 bits each.
We tested all three approaches across a range of compression rates, on different types of neural networks, using different data sets, and we found that in all instances, our approach outperformed the others.
Acknowledgments: Angeliki Metallinou, Inderjit Dhillon