Commercial applications of deep learning have been making headlines for years — never more so than this spring. More surprisingly, deep-learning methods have also shown promise for scientific computing, where they can be used to predict solutions to partial differential equations (PDEs). These equations are often prohibitively expensive to solve numerically; using data-driven methods has the potential to transform both scientific and engineering applications of scientific computing, including aerodynamics, ocean and climate, and reservoir modeling.
A fundamental challenge is that the predictions of deep-learning models trained on physical data typically ignore fundamental physical principles. Such models might, for instance, violate system conservation laws: the solution to a heat transfer problem may fail to conserve energy, or the solution to a fluid flow problem may fail to conserve mass. Similarly, a model’s solution may violate boundary conditions — say, allowing heat flow through an insulator at the boundary of a physical system. This can happen even when the model’s training data includes no such violations: at inference time, the model may simply extrapolate from patterns in the training data in an illicit way.
In a pair of recent papers accepted at the International Conference on Machine Learning (ICML) and the International Conference on Learning Representations (ICLR), we investigate the problems of adding known physics constraints to the predictive outputs of machine learning (ML) models when computing the solutions to PDEs.
The ICML paper, “Learning physical models that can respect conservation laws”, which we will present in July, focuses on satisfying conservation laws with black-box models. We show that, for certain types of challenging PDE problems with propagating discontinuities, known as shocks, our approach to constraining model outputs works better than its predecessors: it more sharply and accurately captures the physical solution and its uncertainty and yields better performance on downstream tasks.
In this paper, we collaborated with Derek Hansen, a PhD student in the Department of Statistics at the University of Michigan, who was an intern at AWS AI Labs at the time, and Michael Mahoney, an Amazon Scholar in Amazon’s Supply Chain Optimization Technologies organization and a professor of statistics at the University of California, Berkeley.
In a complementary paper we presented at this year’s ICLR, “Guiding continuous operator learning through physics-based boundary constraints”, we, together with Nadim Saad, an AWS AI Labs intern at the time and a PhD student at the Institute for Computational and Mathematical Engineering (ICME) at Stanford University, focus on enforcing physics through boundary conditions. The modeling approach we describe in this paper is a so-called constrained neural operator, and it exhibits up to a 20-fold performance improvement over previous operator models.
So that scientists working with models of physical systems can benefit from our work, we’ve released the code for the models described in both papers (conservation laws | boundary constraints) on GitHub. We also presented on both works in March 2023 at AAAI's symposium on Computational Approaches to Scientific Discovery.
Conservation laws
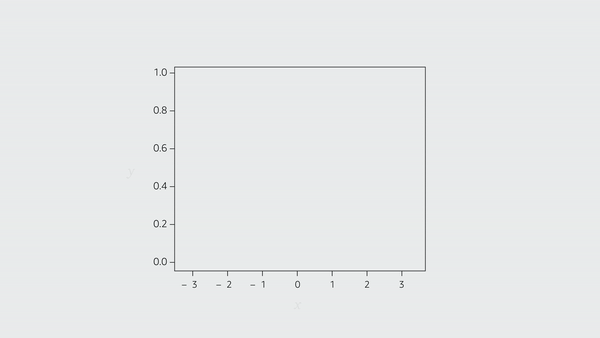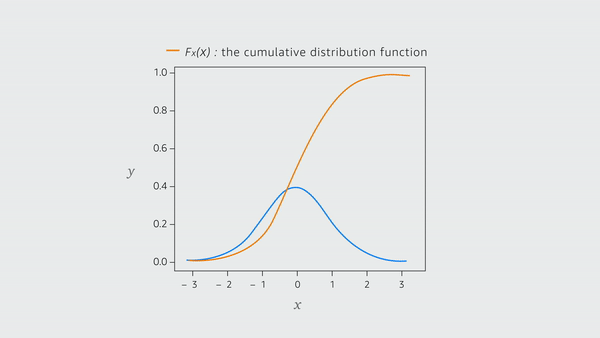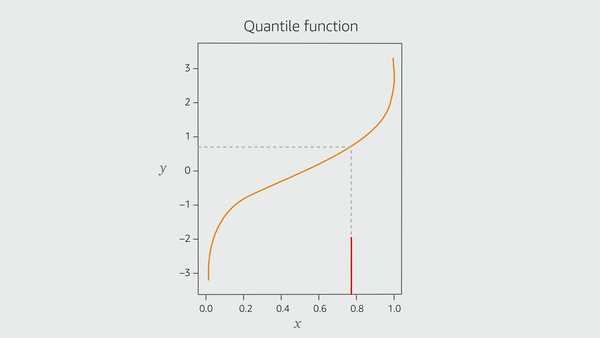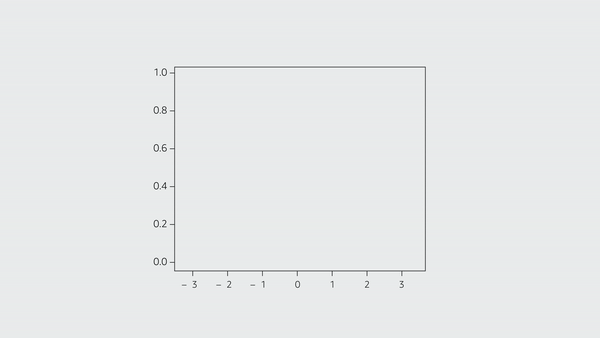
Recent work in scientific machine learning (SciML) has focused on incorporating physical constraints into the learning process as part of the loss function. In other words, the physical information is treated as a soft constraint or regularization.
A main issue with these approaches is that they do not guarantee that the physical property of conservation is satisfied. To address this issue, in “Learning physical models that can respect conservation laws”, we propose ProbConserv, a framework for incorporating constraints into a generic SciML architecture. Instead of expressing conservation laws in the differential forms of PDEs, which are commonly used in SciML as extra terms in the loss function, ProbConserv converts them into their integral form. This allows us to use ideas from finite-volume methods to enforce conservation.
In finite-volume methods, a spatial domain — say, the region through which heat is propagating — is discretized into a finite set of smaller volumes called control volumes. The method maintains the balance of mass, energy, and momentum throughout this domain by applying the integral form of the conservation law locally across each control volume. Local conservation requires that the out-flux from one volume equals the in-flux to an adjacent volume. By enforcing the conservation law across each control volume, the finite-volume method guarantees global conservation across the whole domain, where the rate of change of the system’s total mass is given by the change in fluxes along the domain boundaries.
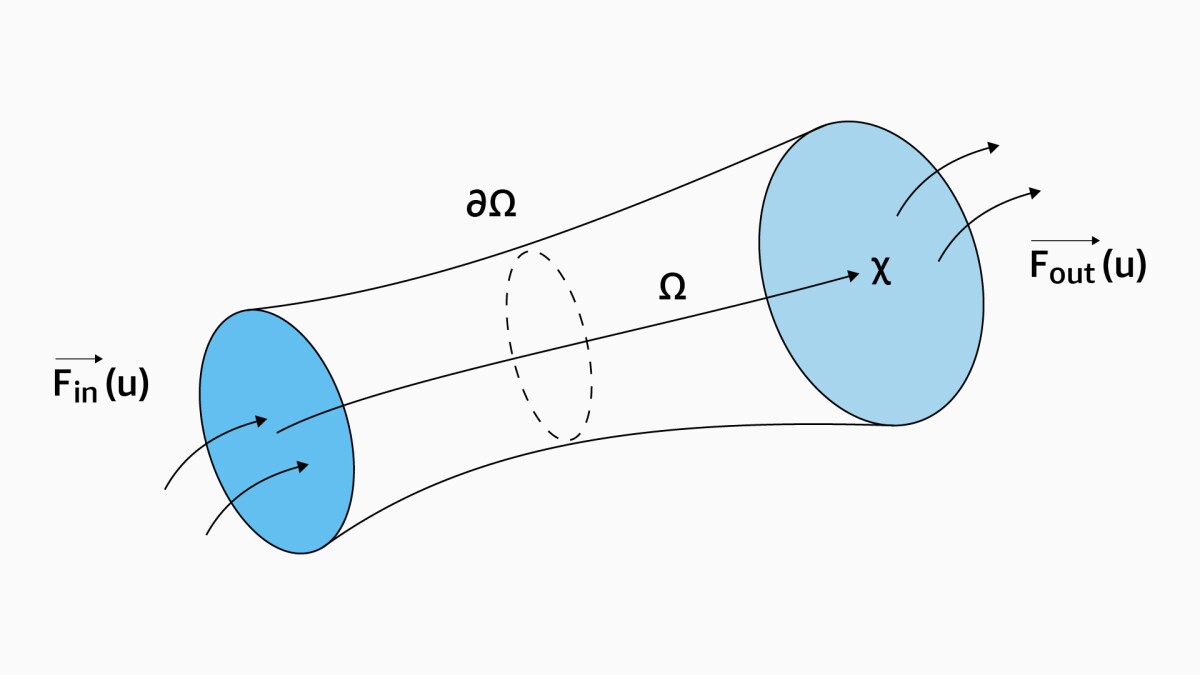
More specifically, the first step in the ProbConserv method is to use a probabilistic machine learning model — such as a Gaussian process, attentive neural process (ANP), or ensembles of neural-network models — to estimate the mean and variance of the outputs of the physical model. We then use the integral form of the conservation law to perform a Bayesian update to the mean and covariance of the distribution of the solution profile such that it satisfies the conservation constraint exactly in the limit.
In the paper, we provide a detailed analysis of ProbConserv’s application to the generalized porous-medium equation (GPME), a widely used parameterized family of PDEs. The GPME has been used in applications ranging from underground flow transport to nonlinear heat transfer to water desalination and beyond. By varying the PDE parameters, we can describe PDE problems with different levels of complexity, ranging from “easy” problems, such as parabolic PDEs that model smooth diffusion processes, to “hard” nonlinear hyperbolic-like PDEs with shocks, such as the Stefan problem, which has been used to model two-phase flow between water and ice, crystal growth, and more complex porous media such as foams.
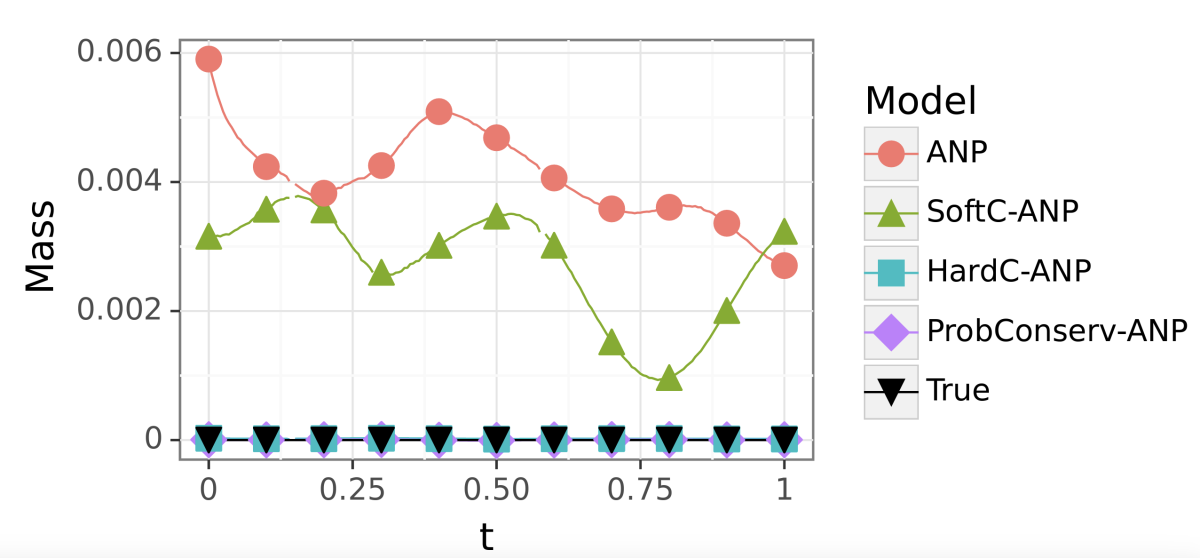
For easy GPME variants, ProbConserv compares well to state-of-the-art competitors, and for harder GPME variants, it outperforms other ML-based approaches that do not guarantee volume conservation. ProbConserv seamlessly enforces physical conservation constraints, maintains probabilistic uncertainty quantification (UQ), and deals well with the problem of estimating shock propagation, which is difficult given ML models’ bias toward smooth and continuous behavior. It also effectively handles heteroskedasticity, or fluctuation in variables’ standard deviations. In all cases, it achieves superior predictive performance on downstream tasks, such as predicting shock location, which is a challenging problem even for advanced numerical solvers.
Examples
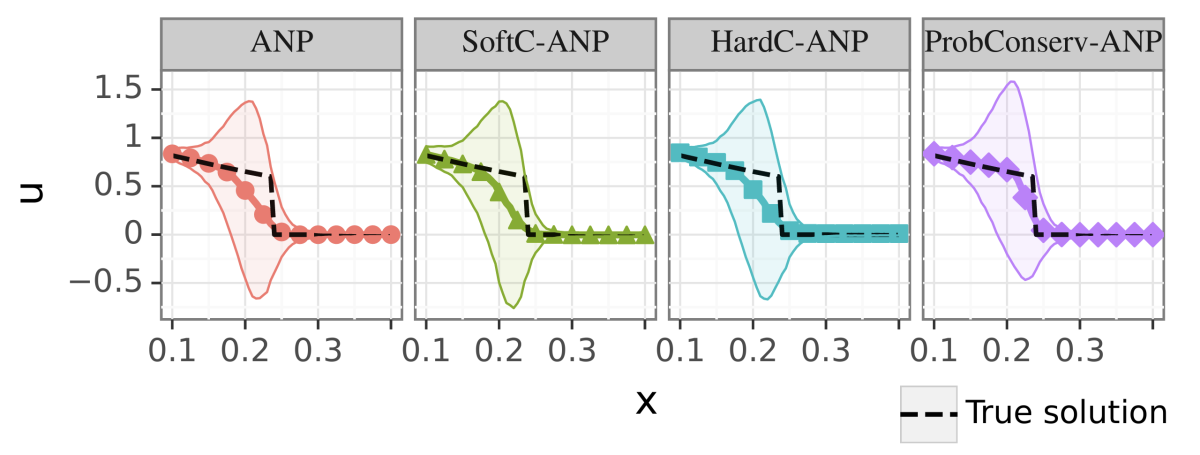
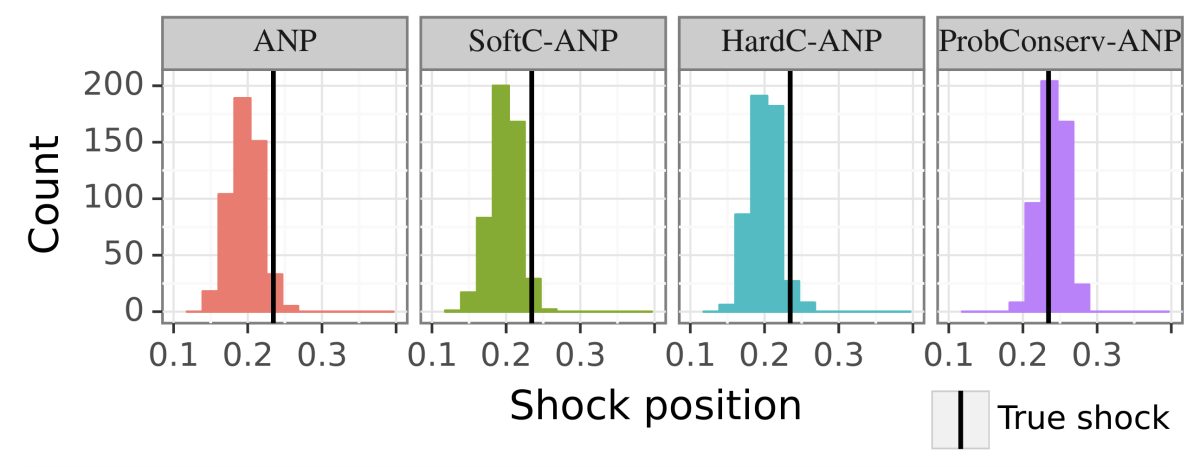
Boundary conditions
Boundary conditions (BCs) are physics-enforced constraints that solutions of PDEs must satisfy at specific spatial locations. These constraints carry important physical meaning and guarantee the existence and the uniqueness of PDE solutions. Current deep-learning-based approaches that aim to solve PDEs rely heavily on training data to help models learn BCs implicitly. There is no guarantee, though, that these models will satisfy the BCs during evaluation. In our ICLR 2023 paper, “Guiding continuous operator learning through physics-based boundary constraints”, we propose an efficient, hard-constrained, neural-operator-based approach to enforcing BCs.
Where most SciML methods (for example, PINNs) parameterize the solution to PDEs with a neural network, neural operators aim to learn the mapping from PDE coefficients or initial conditions to solutions. At the core of every neural operator is a kernel function, formulated as an integral operator, that describes the evolution of a physical system over time. For our study, we chose the Fourier neural operator (FNO) as an example of a kernel-based neural operator.
We propose a model we call the boundary-enforcing operator network (BOON). Given a neural operator representing a PDE solution, a training dataset, and prescribed BCs, BOON applies structural corrections to the neural operator to ensure that the predicted solution satisfies the system BCs.
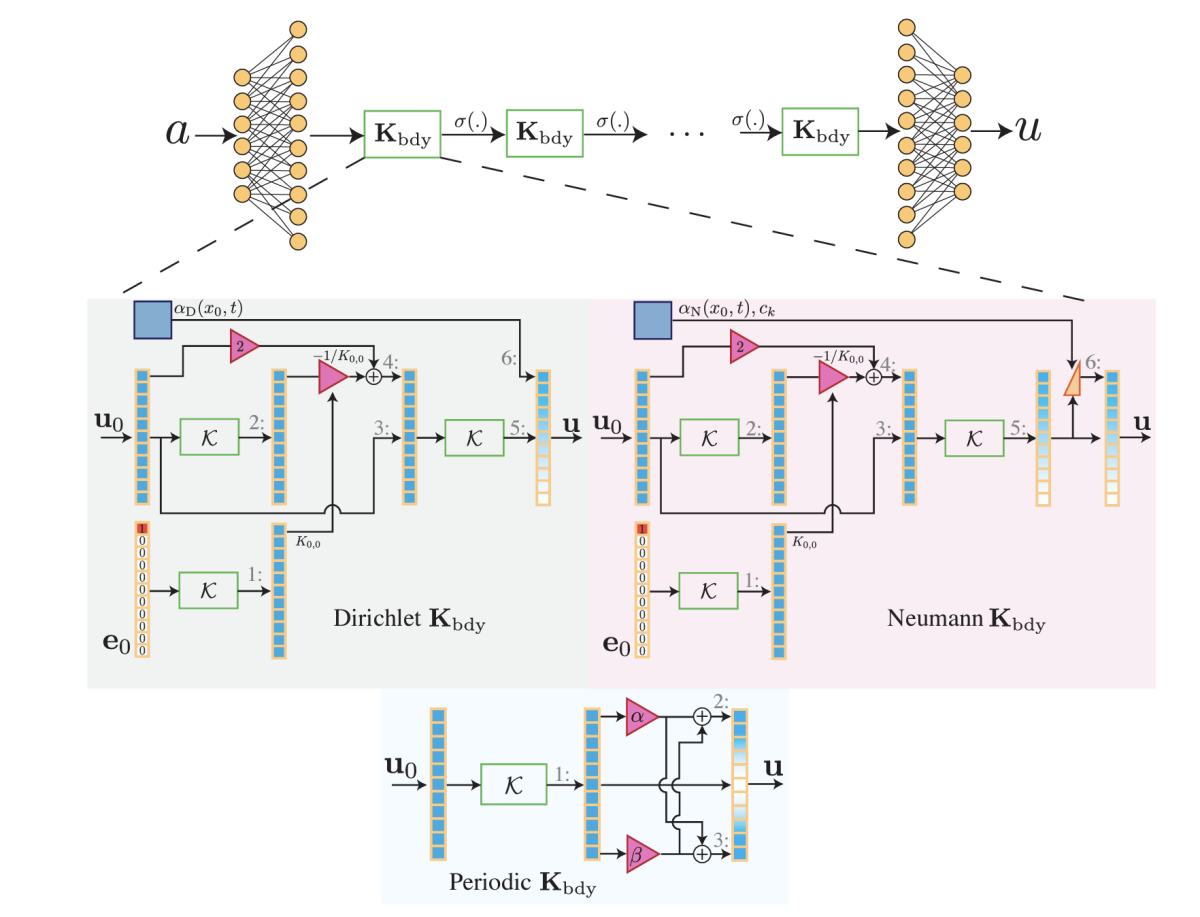
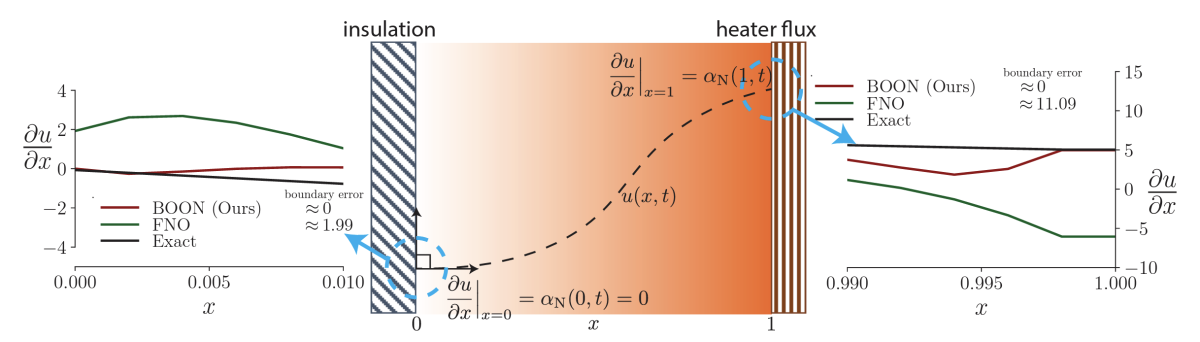
We provide our refinement procedure and demonstrate that BOON’s solutions satisfy physics-based BCs, such as Dirichlet, Neumann, and periodic. We also report extensive numerical experiments on a wide range of problems including the heat and wave equations and Burgers's equation, along with the challenging 2-D incompressible Navier-Stokes equations, which are used in climate and ocean modeling. We show that enforcing these physical constraints results in zero boundary error and improves the accuracy of solutions on the interior of the domain. BOON’s correction method exhibits a 2-fold to 20-fold improvement over a given neural-operator model in relative L2 error.
Examples


Acknowledgements: This work would have not been possible without the help of our coauthor Michael W. Mahoney, an Amazon Scholar; coauthors and PhD student interns Derek Hansen and Nadim Saad; and mentors Yuyang Wang and Margot Gerritsen.