Last week, the Alexa Auto team announced the release of its new Alexa Auto Software Development Kit (SDK), enabling developers to bring Alexa functionality to in-vehicle infotainment systems.

The initial release of the SDK assumes that automotive systems will have access to the cloud, where the machine-learning models that power Alexa currently reside. But in the future, we would like Alexa-enabled vehicles — and other mobile devices — to have recourse to some core functions even when they’re offline. That will mean drastically reducing the size of the underlying machine-learning models, so they can fit in local memory.
At the same time, third-party developers have created more than 45,000 Alexa skills, which expand on Alexa’s native capabilities, and that number is increasing daily. Even in the cloud, third-party skills are loaded into memory only when explicitly invoked by a customer request. Shrinking the underlying models would reduce load time, ensuring that Alexa customers continue to experience millisecond response times.
At this year’s Interspeech, my colleagues and I will present a new technique for compressing machine-learning models that reduces their memory footprints by 94% while leaving their performance almost unchanged. We report our results in a paper titled “Statistical model compression for small-footprint natural language understanding.”
Quantization
Alexa’s natural-language-understanding systems, which interpret free-form utterances, use several different types of machine-learning (ML) models, but they all share some common traits. One is that they learn to extract “features” — or strings of text with particular predictive value — from input utterances. An ML model trained to handle music requests, for instance, will probably become sensitized to text strings like “the Beatles”, “Elton John”, “Whitney Houston”, “Adele”, and so on. Alexa’s ML models frequently have millions of features.
Another common trait is that each feature has a set of associated “weights,” which determine how large a role it should play in different types of computation. The need to store multiple weights for millions of features is what makes ML models so memory intensive.
Our first technique for compressing an ML model is to quantize its weights. We take the total range of weights — say, -100 to 100 — and divide it into even intervals — say, -100 to -90, -90 to -80, and so on. Then we simply round each weight off to the nearest boundary value for its interval. In practice, we use 256 intervals, which allows us to represent every weight in the model with a single byte of data, with minimal effect on the network’s accuracy. This approach has the added benefit of automatically rounding low weights to zero, so they can be discarded.
Perfect hashing
Our other compression technique is more elegant. If an Alexa customer says, “Alexa, play ‘Yesterday,’ by the Beatles,” we want our system to pull up the weights associated with the feature “the Beatles” — not the weights associated with “Adele”, “Elton John”, and the rest. This requires a means of mapping particular features to the memory locations of the corresponding weights.
The standard way to perform such mappings is through hashing. A hash function is a mathematical function that takes arbitrary inputs and scrambles them up — hashes them — in such a way that the outputs (1) are of fixed size and (2) bear no predictable relationship to the inputs. If the output size is fixed at 16 bits, for instance, there are 65,536 possible hash values, but “Hank Williams” might map to value 1, while “Hank Williams, Jr.” maps to value 65,000.
Nonetheless, traditional hash functions sometimes produce collisions: Hank Williams, Jr. may not map to the same location as Hank Williams, but something totally arbitrary — the Bay City Rollers, say — might. In terms of runtime performance, this usually isn’t a big problem. If you hash the name “Hank Williams” and find two different sets of weights at the corresponding memory location, it doesn’t take that long to consult a metadata tag to determine which set of weights belongs to which artist.
In terms of memory footprint, however, this approach to collision resolution makes a substantial difference. With quantizing, the weights themselves will require just a few bytes of data; the metadata used to distinguish sets of weights could end up requiring more space in memory than the data it’s tagging.
We address this problem by using a more advanced hashing technique called perfect hashing, which maps a specific number of data items to the same number of memory slots but guarantees there will be no collisions. With perfect hashing, the system can simply hash a string of characters and pull up the corresponding weights — no metadata required.
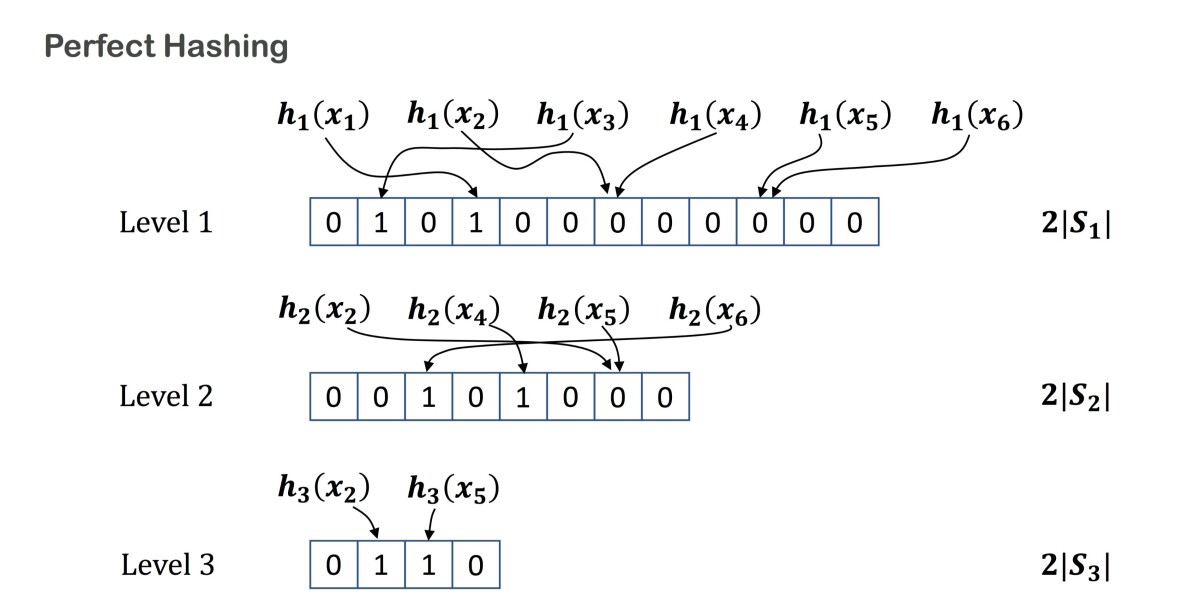
To produce a perfect hash, we assume that we have access to a family of conventional hash functions all of which produce random hashes. That is, each function in the family might hash “Hank Williams” to a different value, but that value tells you nothing about how the same function will hash any other string. In practice, we use the hash function MurmurHash, which can be seeded with a succession of different values.
Suppose that you have N input strings that you want to hash. We begin with an array of N 0’s. Then we apply our first hash function — call it Hash1 — to all N inputs. For every string that yields a unique hash value — no collisions — we change the corresponding 0 in the array to a 1.
Then we build a new array of 0’s, with entries for only the input strings that yielded collisions under Hash1. To those strings, we now apply a different hash function — say, Hash2 — and we again toggle the 0’s corresponding to collision-free hashes.
We repeat this process until every input string has a corresponding 1 in some array. Then we combine all the arrays into one giant array. The position of a 1 in the giant array indicates the unique memory location assigned to the corresponding input string.
Now, when the trained network receives an input, it applies Hash1 to each of the input’s substrings and, if it finds a 1 in the first array, it goes to the associated address. If it finds a 0, it applies Hash2 and repeats the process.
Calling successive hash functions for some inputs does incur a slight performance penalty. But it’s a penalty that’s paid only where a conventional hash function would yield a collision, anyway. In our paper, we include both a theoretical analysis and experimental results that demonstrate that this penalty is almost negligible. And it’s certainly a small price to pay for the drastic reduction in memory footprint that the method affords.
Acknowledgments: Kanthashree Mysore Sathyendra, Stanislav Peshterliev