Gradient-boosted decision trees are a machine learning model commonly used in large-scale, online search applications because they combine high accuracy with high efficiency.
Maintaining that efficiency, however, means limiting the number of data features that gradient-boosted trees consider in making a decision. If the training data for a decision tree model has many possible features to choose from — say, thousands — and the model will end up using only a fraction of them — say, a couple hundred — then training can become inefficient, as most of the features the model evaluates will prove irrelevant.
In a paper accepted to the International Conference on Artificial Intelligence and Statistics, which was to be held last week but has been postponed until September, we present a new method for training gradient-boosted trees that is much more efficient than its most efficient predecessor in cases where the total feature set is larger than the necessary-feature set.
In tests, we compared our approach to three other implementations of gradient-boosted decision trees, using three popular benchmark data sets. Relative to the most efficient of its predecessors — a technique called gradient-boosted feature selection — our method reduced training time by 50% to 99%, while preserving the accuracy of the resulting models.
We also found that our approach is particularly well suited to multitask training, in which the machine learning model is trained to perform several tasks at once — identifying images of dogs, cats, and horses, for instance, instead of just one of the three.
In experiments, when our system was trained on three tasks simultaneously, it performed better on each of those tasks than when it was trained on a single task. We also compared it to the standard method of doing multitask training with gradient-boosted trees and found that it improved performance on all three tasks.
A decision tree is a binary tree — something like a flow chart — that presents a series of binary decisions. With each decision, the tree branches into two paths. Ultimately, every path through the tree reaches a terminal point known as a leaf. Each leaf has an associated number that represents its vote on some classification task: yes, I think this is a dog; no, I don’t think this song is a good match for the query.
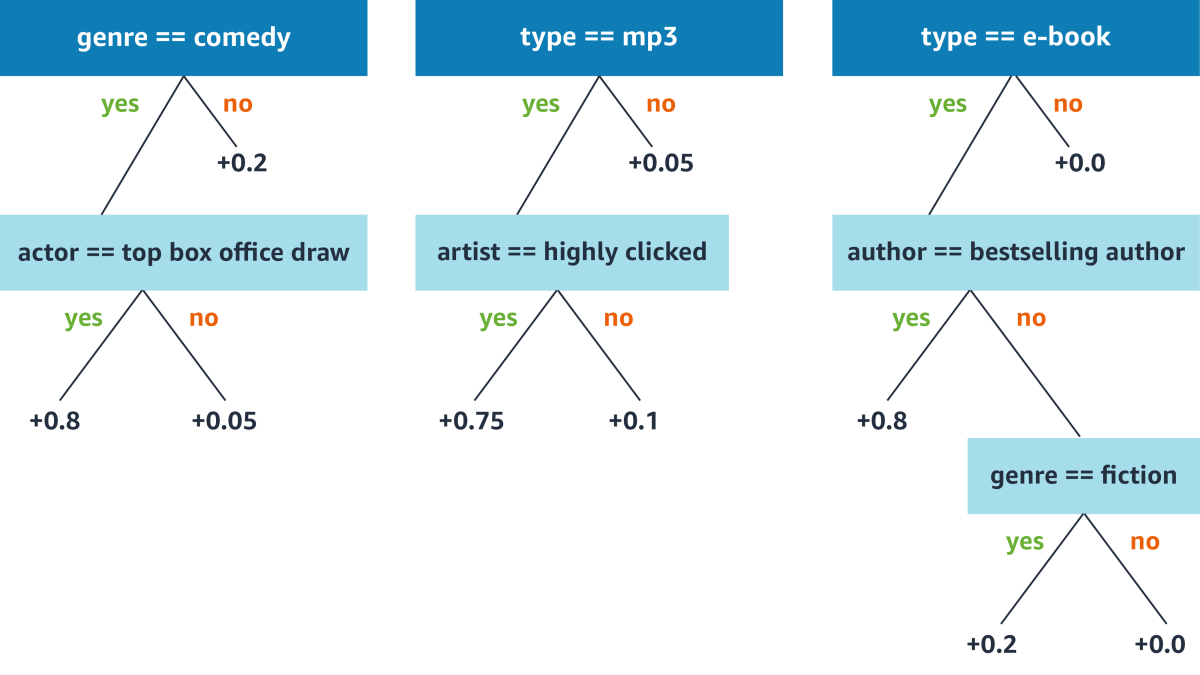
A model that uses gradient-boosted decision trees consists of multiple trees — possibly hundreds. During training, the model builds the trees in sequence. Each new tree is designed to minimize the residual error of the trees that preceded it: that’s the gradient boosting. The output of the model as a whole is the aggregate output of all the trees.
At each new decision point for each tree, the model has to select a decision criterion that will minimize the error rate of the model as a whole. That means evaluating every possible feature of the training data — in the case of a music track, artist, title, genre, date of release, bit rate, track number, and so on.
For each of those features, the model must find the best split point, the threshold value that determines whether the path branches left or right. If the data has 1,000 features, but only 100 of them will ultimately prove useful as decision criteria, most of that work is wasted.
Collective action
We address this problem by adapting the common binary-search algorithm. Before training, we normalize the values for each feature, so that they all fall within the range of 0 to 1. Then we randomly divide the features into two groups, creating two pseudo-features, whose values are simply the sums of the normalized values for the individual features. We repeat this process several times, producing several pairs of pseudo-features that evenly divide the feature set.
During training, at each decision point, we evaluate the tree using one pair of pseudo-features, selecting a split point for each in the ordinary fashion. We then take the pseudo-feature that leads to better prediction, randomly divide it into two new pseudo-features, and again test split points.
We repeat this process until we’ve converged on a single feature to serve as the criterion for that decision point. Rather than evaluate every feature, we evaluate a number of pseudo-features equal to the logarithm of the number of features.
This approach is only an approximation, but in the paper, we present a theoretical analysis showing that, given enough training data, the approximation should still converge on an optimal set of decision trees.
We also tested our approach empirically, on three standard benchmarks for machine learning research. One is a data set of handwritten numbers, and the goal is to identify the numbers; another is a data set of flight information, and the goal is to predict delays; and the third is an image recognition task. We compared our system’s performance to that of three other standard implementations of gradient-boosted trees.
In all cases, our system’s performance was within a fraction of a percentage point of the best-performing baseline’s — either ahead or behind — but its training time was much lower. The differences in training time varied depending on the systems’ target accuracy rate, but for the flight data set, the training time acceleration was consistently around twofold; for the handwriting recognition task, it was consistently around 10-fold; and for the image recognition task, it was consistently around 100-fold.

















