Large language models (LLMs) go through several stages of training on mixed datasets with different distributions, stages that include pretraining, instruction tuning, and reinforcement learning from human feedback. Finding the optimal mix of data distributions across datasets is essential to building accurate models, but it typically requires training and evaluating the model numerous times on a very large set of combinations.
At the last Conference on Empirical Methods in Natural-Language Processing (EMNLP), my colleagues and I proposed a training framework that reduces the computational cost of using mixed data distributions to train LLMs or other neural-network-based models by up to 91%. At the same time, the method actually improves the quality of the resulting models.
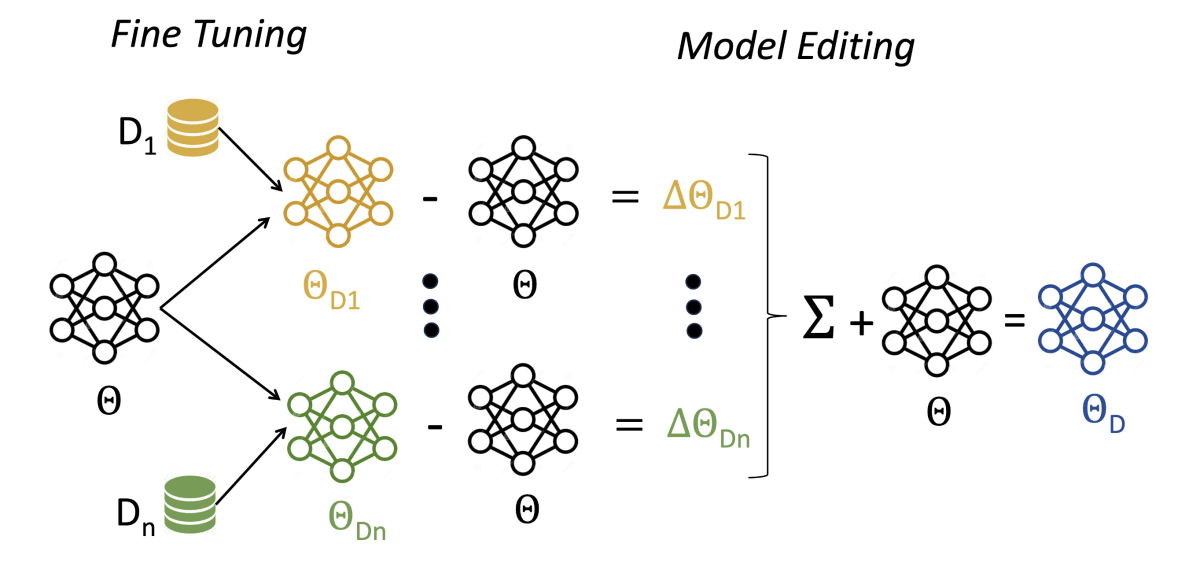
Whereas the standard approach to optimizing data distributions involves weighting the different datasets used to train a single model, we train a separate model on each dataset and then weight the models to produce a composite model.
This unconventional approach won a special award for “efficient modeling, training, and inference” at EMNLP and has the potential to make large-model training much more efficient and accessible.
Distribution-edited models
Traditional training approaches (e.g., instruction tuning) select the optimal mix of training data distributions through a method called grid search, an exhaustive-search method that simply compares outcomes for a wide range of different weight values. This is very demanding not only in terms of time and resources but also in terms of flexibility: once the model is trained, it can’t be changed without incurring similar costs.
To address these limitations, we propose fine-tuning a pretrained model on data distributions that correspond to different tasks and then subtracting the parameter values of the original model from those of the fine-tuned models. We call the differences in parameter values distribution vectors, and we produce a composite model by adding a weighted sum of distribution vectors to the parameters of the original model.
We call the resulting model a distribution-edited model (DEM) to highlight the leveraging of weight vector arithmetic for model editing. The weights are based on the perplexity of each fine-tuned model, or the probability that its parameter values can be predicted from those of the original model.
This approach relies on two key observations: (1) training the model separately on each dataset allows better modeling of each dataset’s underlying properties, as there is no interference with other data distributions during the training process; and (2) perplexity can be computed in a single forward pass on validation data, which is much more efficient than grid search. The first point helps improve model quality, and the second point helps make training much more efficient.
In more detail, here are the steps in the approach:
- Individual-distribution training: The original model is trained on individual data distributions through standard training procedures. Checkpoints, or snapshots of the model state after training on a particular dataset, are stored for subsequent steps.
- Distribution vector computation: Distribution vectors are computed by subtracting the pretrained model's parameters from those of the fine-tuned models. These vectors capture the unique characteristics of each dataset.
- Optimization of merging coefficients: The optimal coefficients for combining the data distribution vectors are found based on perplexity on the validation set using a single forward pass per combination.
- Merging of distribution vectors: Linearly combining the distribution vectors with customizable weights creates a unified model that effectively captures the joint distribution of diverse datasets.
- Resulting properties (flexibility and scalability): DEM enables incremental updates when new datasets are introduced, without requiring full retraining. This makes it ideal for dynamic and large-scale training scenarios.
Evaluation and future work
In evaluating our approach, we focused on training LLMs of increasing size, from 3 billion parameters up to 13 billion parameters, during the instruction-tuning stage. Our study showed that DEM reduces training costs by up to 91% while achieving up to 16.1% quality improvement over traditional data-mixing strategies, highlighting DEM’s potential to democratize access to state-of-the-art training techniques and offer transformative benefits to organizations leveraging neural models at scale. In addition, DEM’s flexibility ensures that researchers and practitioners can quickly adapt to new data requirements without compromising performance.
The key takeaways from the study can be summarized as follows:
- Superior performance: DEM has been validated on popular benchmarks like MMLU, BBH, and HELM, where it achieved up to 16.1% improvement over data mixing on individual tasks.
- Diverse domain effectiveness: Experiments on datasets such as MathQA, Super-Natural Instructions (SNI), and Chain-of-Thought (CoT) demonstrate DEM’s ability to excel across a variety of domains.
- Scalability: DEM is shown to improve performance at different model sizes — 3B, 7B and 13B — providing strong evidence for the scalability of this approach.
The effectiveness of DEM underscores the importance of innovation in making machine learning more efficient and accessible. As the machine learning community continues to scale models and datasets, frameworks like DEM will be essential for maintaining efficiency without sacrificing performance. Future research may explore the effectiveness of the framework on other training scenarios and its extension to other model architectures, such as encoder-decoder frameworks or mixture-of-experts models.