Most of today’s breakthrough AI models are based on the transformer architecture, which is distinguished by its use of an attention mechanism. In a large language model (LLM), for instance, the transformer decides which words in the text string to pay particular attention to when generating the next word; in a vision-language model, it might decide which words of an instruction to attend to when computing pixel values.
Given the increasing importance of transformer models, we naturally want to better understand their dynamics — whether the training process will converge on a useful model, for instance, and how fast, or which architectural variations work best for what purposes. The complexity of the attention mechanism, however, makes traditional analytic tools difficult to apply.
Last week, at the 2024 Conference on Neural Information Processing Systems (NeurIPS), we presented a new analysis of the transformer architecture. First, we identified hyperparameters and initialization conditions that provide a probabilistic guarantee of convergence to a globally optimal solution.
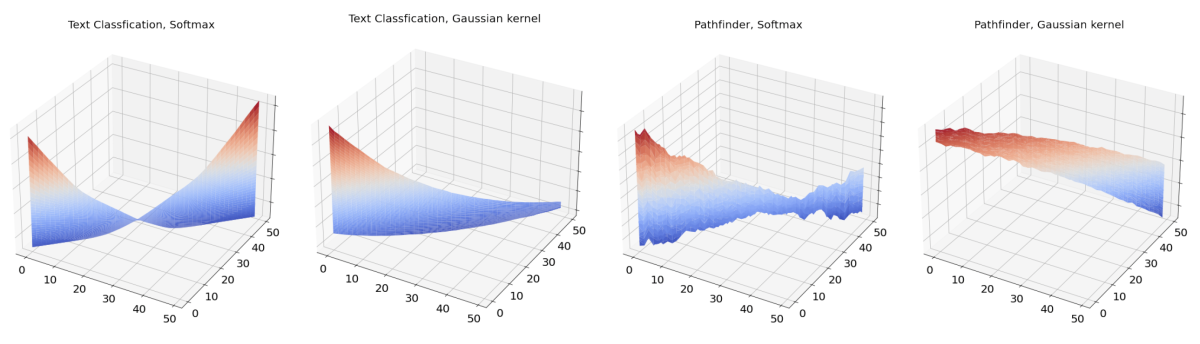
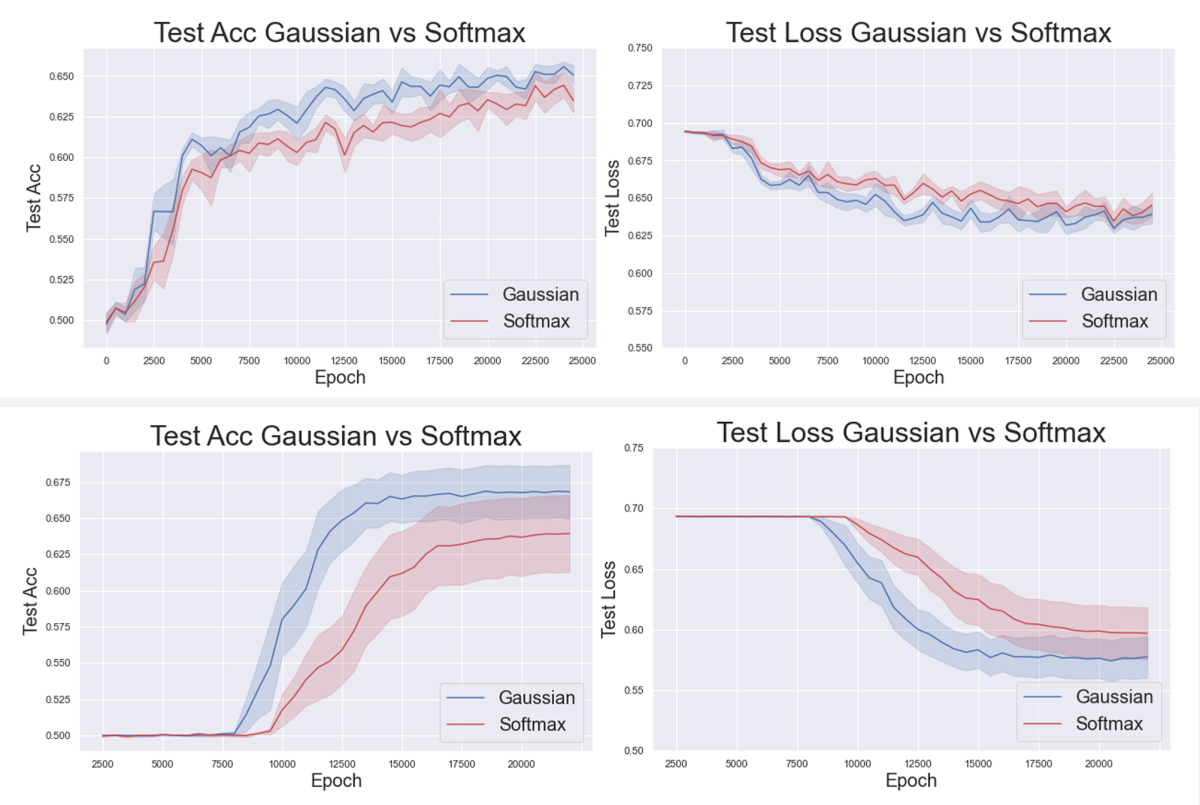
Through ablation studies, we also showed that the choice of attention kernel — the function used to compute the attention weights — influences the convergence rate. Specifically, the Gaussian kernel will sometimes enable convergence when the more common softmax kernel will not. Finally, we conducted an empirical study that showed that, in some specific settings, models trained using the Gaussian kernel converged more rapidly than models trained using the softmax kernel, due to a smoother optimization landscape.
A tale of three matrices
In a transformer, the attention weight computation involves three matrices: the query matrix, the key matrix, and the value matrix. All three are used to produce encodings of input data. In a self-attention mechanism, which compares an input to itself (as in the case of LLMs), the query and key matrices are applied to the same input. In a cross-attention mechanism, they’re applied to different inputs: in a multimedia model, for instance, one matrix may be used to encode texts, while the other is used to encode images.
The attention kernel defines an operation performed on the query and key encodings; the result of the operation indicates the relevance of one of set of inputs to another (or to itself). The encoding produced by the value matrix represents semantic properties of the data. The result of the kernel operation is multiplied by the encodings produced by the value matrix, emphasizing some semantic features and deemphasizing others. The result is, essentially, a recipe for the semantic content of the model’s next output.
Typically, during model training, all three matrices are updated together. But we analyzed the results of updating only subsets of the matrices while the others remain fixed. This enabled us to identify which matrices and kernel functions exert the largest influence on convergence rate. The results were as follows:
- If all three matrices can be updated, ordinary gradient descent (GD) can achieve global optimality, with either Gaussian or softmax attention kernels;
- If only the value matrix can be updated, GD is still optimal, with either kernel;
- If only the query matrix can be updated, GD convergence is guaranteed only with the Gaussian kernel.
This suggests that in some cases, the commonly used softmax kernel may have drawbacks, and we conducted a set of experiments that bear that intuition out. On two different datasets — one for a text classification task and one for an image interpretation and segmentation task — we trained pairs of transformer models, one with a Gaussian kernel and one with a softmax kernel. On both tasks, the Gaussian kernel enabled faster convergence rates and higher accuracy in the resulting model.
Our analysis also indicates that, theoretically, convergence depends centrally on updates to the value matrix, since the multiplication of the value matrix and the results of the kernel operation is a linear operation, whereas the kernel operation is nonlinear.
Finally, our paper also sets out a group of initialization conditions that are necessary to guarantee convergence. These include the requirements that the matrix of the kernel operations have full rank — that is, that its columns are linearly independent — and that the ratio of the query and key matrices’ eigenvalues to the value matrix’s eigenvalue fall above a specified threshold.
Further details can be found in our paper. We hope that other members of the AI community will expand on our analyses, expanding our understanding of transformers as they play a larger and larger role in our everyday lives.

















